প্রশ্ন: 18 মিটার দীর্ঘ একটি মই ভূমির সাথে 45° কোণে হেলান দিয়ে একটি দেয়ালের ছাদ স্পর্শ করে। দেয়ালটির উচ্চতা কত?

সমাধান: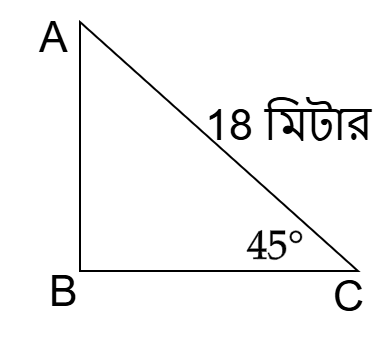

এখানে, মইটির দৈর্ঘ্য (অতিভুজ), AC = 18 মিটার।
ভূমির সাথে উৎপন্ন কোণ, ∠ACB = 45°
দেয়ালের উচ্চতা (লম্ব), AB = ?

আমরা জানি,
sinθ = লম্ব/অতিভুজ
বা, sin45° = AB/AC
বা, 1/√2 = AB/18
বা, √2AB = 18
বা, AB = 18/√2
বা, AB = (18 × √2)/(√2 × √2)
বা, AB = (18√2)/2
∴ AB = 9√2 মিটার

সুতরাং, দেয়ালটির উচ্চতা 9√2 মিটার।

প্রশ্ন: একটি 12 সেমি ব্যাস এবং 9 সেমি উচ্চতা বিশিষ্ট বেলন থেকে গলিত ধাতু দিয়ে 9টি অভিন্ন গোলক তৈরি করা হলে প্রতিটি গোলকের ব্যাস কত?

সমাধান:
মনে করি,
প্রতিটি গোলকের ব্যাসার্ধ = r সেমি।

দেয়া আছে,
বেলনের ব্যাস = 12 সেমি।
∴ বেলনের ব্যাসার্ধ, R = 12/2 = 6 সেমি।
বেলনের উচ্চতা, h = 9 সেমি।

আমরা জানি,
গোলকের আয়তন = (4/3)πr3
বেলনের আয়তন = πR2h

প্রশ্নমতে,
9টি গোলকের মোট আয়তন = 1টি বেলনের আয়তন।
⇒ 9 × (4/3) × π × r3 = π × R2 × h
⇒ 12 × π × r3 = π × 62 × 9
⇒ 12πr3 = π × 36 × 9
⇒ 12πr3 = 324 π
⇒ 12r3 = 324
⇒ r3 = 324/12
⇒ r3 = 27
⇒ r = 3 সেমি

∴ প্রতিটি গোলকের ব্যাসার্ধ = 3 সেমি।
∴ প্রতিটি গোলকের ব্যাস = 2 × ব্যাসার্ধ = 2 × 3 = 6 সেমি।