একটি স্কুলে ৭৫% ছাত্র নিয়মিত হোমওয়ার্ক করে এবং যেসব ছাত্র নিয়মিত হোমওয়ার্ক করে তাদের মধ্যে ৮০% ছাত্র পরীক্ষায় উত্তীর্ণ হয়। তাহলে দৈবভাবে নির্বাচিত একজন ছাত্র পরীক্ষায় উত্তীর্ণ হওয়ার সম্ভাবনা কত?
A
০.৬
B
০.৩
C
০.০৬
D
০.০৪
উত্তরের বিবরণ
প্রশ্ন: একটি স্কুলে ৭৫% ছাত্র নিয়মিত হোমওয়ার্ক করে এবং যেসব ছাত্র নিয়মিত হোমওয়ার্ক করে তাদের মধ্যে ৮০% ছাত্র পরীক্ষায় উত্তীর্ণ হয়। তাহলে দৈবভাবে নির্বাচিত একজন ছাত্র পরীক্ষায় উত্তীর্ণ হওয়ার সম্ভাবনা কত?
সমাধান:
ধরি,
মোট ছাত্র = ১০০ জন
নিয়মিত হোমওয়ার্ক করে এমন ছাত্র = ৭৫% = ৭৫ জন
তাদের মধ্যে ৮০% উত্তীর্ণ হয় অর্থাৎ = (৮০/১০০) × ৭৫ = ৬০ জন
সুতরাং, উত্তীর্ণ ছাত্র = ৬০ জন
∴ একজন দৈবচয়নে নেওয়া ছাত্র উত্তীর্ণ হওয়ার সম্ভাবনা = ৬০/১০০ = ৩/৫ = ০.৬
0
Updated: 1 month ago
(xa/xb)(a + b) (xb/xc)(b + c) (xc/xa)(c + a) এর মান কত?
Created: 2 months ago
A
0
B
1
C
- 1
D
1/2
প্রশ্ন: (xa/xb)(a + b) (xb/xc)(b + c) (xc/xa)(c + a) এর মান কত?
সমাধান: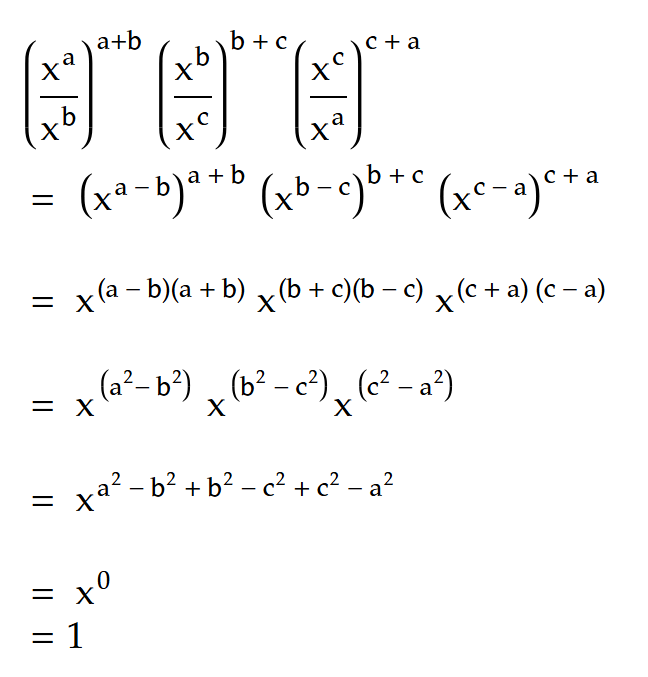
0
Updated: 2 months ago
a-3 = 0.5 হলে
a18 = কত?
Created: 2 months ago
A
18
B
12
C
32
D
64
সমাধান:
দেওয়া আছে,
⇒ a- 3 = 0.5
⇒ 1/a3 = 5/10
⇒ a3 = 2
⇒ (a3)6 = 26
∴ a18 = 64
0
Updated: 2 months ago
a+b+c = 9, a²+b²+c² = 29 হলে, ab+bc+ca এর মান কত?
Created: 1 week ago
A
52
B
46
C
26
D
22
0
Updated: 1 week ago