বৃত্তের কেন্দ্র হতে পরিধি পর্যন্ত দূরত্বকে কী বলা হয়?
A
ব্যাস
B
জ্যা
C
রেখা
D
ব্যাসার্ধ
উত্তরের বিবরণ
প্রশ্ন: বৃত্তের কেন্দ্র হতে পরিধি পর্যন্ত দূরত্বকে কী বলা হয়?
সমাধান:
ব্যাসার্ধ (Radius):
- কেন্দ্র হতে পরিধি পর্যন্ত দূরত্বকে বলা হয় ব্যাসার্ধ।
অর্থাৎ, ব্যাসের অর্ধেকই হচ্ছে ব্যাসার্ধ।
- একে r দ্বারা প্রকাশ করা হয়।
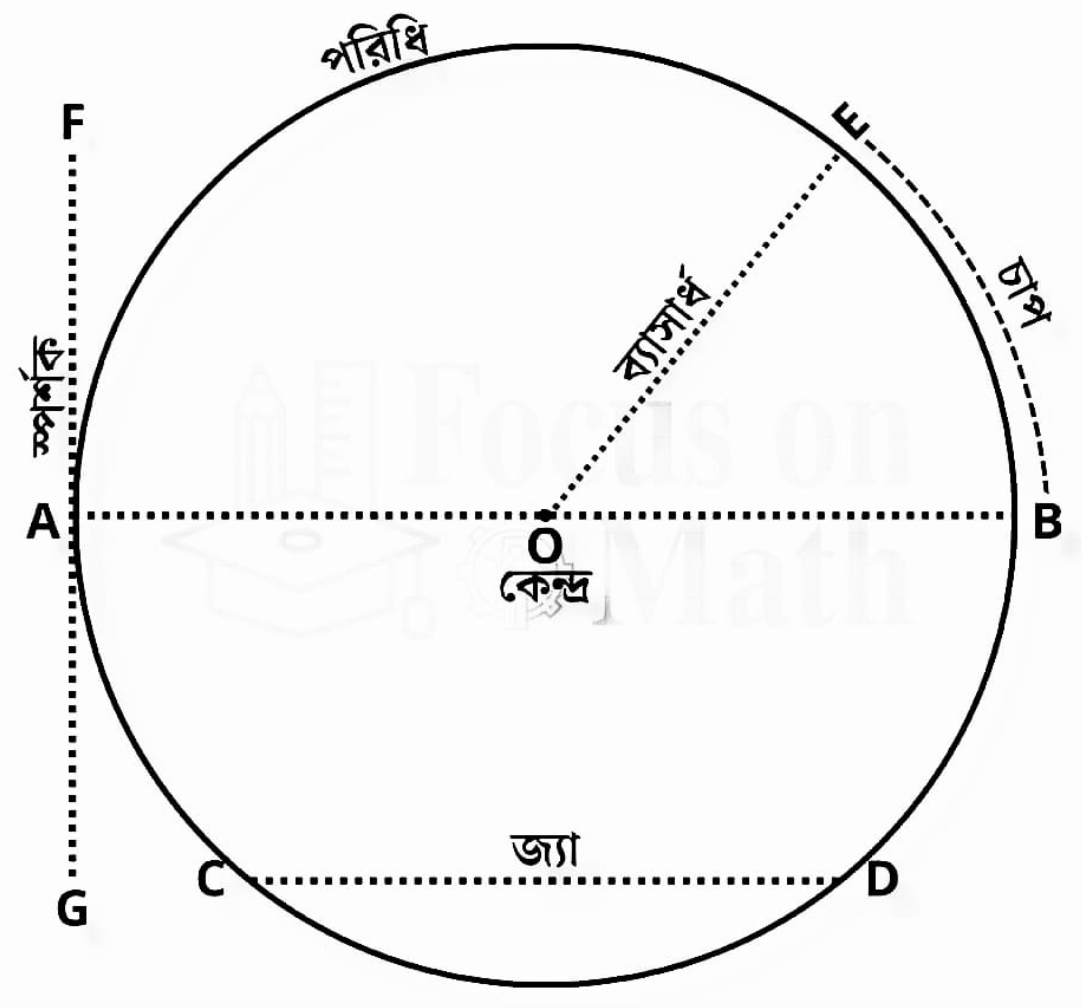
r = বৃত্তের ব্যাসার্ধ (OA = OB = r)।
- ব্যাসার্ধ = ব্যাস/২ = পরিধি/২π = পরিধি × 7/44
- ক্ষেত্রফল = πr2, π = 3.1416....
- ব্যাস : ব্যাসার্ধ = 2 : 1
- বৃত্তের সকল ব্যাসার্ধ সমান।
0
Updated: 1 month ago
ত্রিভুজের মধ্যমার ক্ষেত্রে কোনটি সঠিক নয়?
Created: 2 months ago
A
ত্রিভুজের তিনটি মধ্যমা থাকে
B
মধ্যমা পরস্পরকে ২ : ১ অনুপাতে বিভক্ত করে
C
যে কোনো মধ্যমা ত্রিভুজের ক্ষেত্রফলকে তিন ভাগে ভাগ করে
D
তিনটি মধ্যমা সমান হলে সমবাহু ত্রিভুজ গঠিত হয়
প্রশ্ন: ত্রিভুজের মধ্যমার ক্ষেত্রে কোনটি সঠিক নয়?
সমাধান:
কোনো ত্রিভুজের শীর্ষবিন্দু থেকে ভূমির মধ্যবিন্দুর সংযোগ সরলরেখাকে মধ্যমা বলা হয়।
• ত্রিভুজের তিনটি মধ্যমা থাকে।
• এগুলো সমবিন্দু।
• মধ্যমা পরস্পরকে ২ : ১ অনুপাতে বিভক্ত করে।
• যে কোনো মধ্যমা ত্রিভুজের ক্ষেত্রফলকে সমান দুইভাগে বিভক্ত করে।
• মধ্যমা তিনটি সমান হলে সমবাহু ত্রিভুজ গঠিত হয়।
0
Updated: 2 months ago
y = 3x + 2, y = - 3x + 2 এবং y= - 2 দ্বারা গঠিত জ্যামিতিক চিত্রটি কি?
Created: 5 months ago
A
একটি সমবাহু ত্রিভুজ
B
একটি সমদ্বিবাহু ত্রিভুজ
C
একটি বিষমবাহু ত্রিভুজ
D
একটি সমকোণী ত্রিভুজ
প্রশ্ন: y = 3x + 2, y = - 3x + 2 এবং y= - 2 দ্বারা গঠিত জ্যামিতিক চিত্রটি কি?
সমাধান:
y = 3x + 2……..(i)
y = - 3x + 2…….(ii)
y= - 2……(iii)
এখানে,
(i) ও (ii) নং সমীকরণের ঢাল যথাক্রমে 3 ও -3, যাদের পরমমান সমান।
সুতরাং এই রেখা দুটি সমান।
কিন্তু (iii) নং রেখাটি (i) ও (ii) নং হতে ভিন্ন।
তাই সমীকরণগুলো দ্বারা গঠিত চিত্রটি একটি সমদ্বিবাহু ত্রিভুজ।
বিকল্প:
(i) ও (ii) সরলরেখা দুইটির ছেদবিন্দু (0, 2)
(i) ও (iii) সরলরেখা দুইটির ছেদবিন্দু (- 4/3, - 2)
(ii) ও (iii) সরলরেখা দুইটির ছেদবিন্দু (4/3, - 2)
(0, 2) ও (- 4/3, - 2) বিন্দু দুইটির দূরত্ব = √160/3
(0, 2) ও (4/3, - 2) বিন্দু দুইটির দূরত্ব = √160/3
(- 4/3, - 2) ও (4/3, - 2) বিন্দু দুইটির দূরত্ব = √208/3
y = 3x + 2, y = - 3x + 2 এবং y = - 2 দ্বারা গঠিত জ্যামিতিক চিত্রটি সমদ্বিবাহু ত্রিভুজ।
0
Updated: 5 months ago
একটি
25 মিটার লম্বা মই দেয়ালের সাথে
খাড়া করে রাখা আছে।
মইটির গোড়া দেয়াল থেকে কত দূরে
সরালে এর উপরের অংশ
5 মিটার নিচে নেমে আসবে?
Created: 1 month ago
A
13 মিটার
B
10 মিটার
C
18 মিটার
D
15 মিটার
প্রশ্ন: একটি 25 মিটার লম্বা মই দেয়ালের সাথে খাড়া করে রাখা আছে। মইটির গোড়া দেয়াল থেকে কত দূরে সরালে এর উপরের অংশ 5 মিটার নিচে নেমে আসবে?
সমাধান:
এখানে, AC মইয়ের গোড়া C থেকে D বিন্দুতে সরালে উপরের প্রান্ত A বিন্দু থেকে B বিন্দুতে 5 মিটার নামবে।
মইয়ের দৈর্ঘ্য, AC = BD = 25 মিটার
এবং AB = 5 মিটার
∴ BC = 25 - 5 = 20 মিটার
এখন, পিথাগোরাসের সূত্র অনুযায়ী পাই,
BD2 = BC2 + CD2
⇒ 252 = 202 + CD2
⇒ 625 = 400 + CD2
⇒ CD2 = 625 - 400
⇒ CD2 = 225
⇒ CD = √225
⇒ CD = 15 মিটার
∴ মইটির গোড়া দেয়াল থেকে 15 মিটার দূরে সরালে এর উপরের অংশ 5 মিটার নিচে নেমে আসবে।
0
Updated: 1 month ago