একটি সুষম ষড়ভুজের প্রত্যেকটি কোণের পরিমাণ কত?
A
60°
B
90°
C
120°
D
180°
উত্তরের বিবরণ
প্রশ্ন: একটি সুষম ষড়ভুজের প্রত্যেকটি কোণের পরিমাণ কত?
সমাধান:
সুষম ষড়ভুজের বাহুর সংখ্যা n হলে,
অন্তঃকোণ = {(n - 2) × 180°}/n
= {(6 - 2) ×180°}/6
= (4 ×180°)/6
= 120° ।
0
Updated: 1 month ago
চিত্রে, ∠BEF + ∠EFD = ?
Created: 3 weeks ago
A
360°
B
270°
C
180°
D
90°
চিত্রে, AB || CD এবং PQ ছেদক এদের যথাক্রমে E ও F বিন্দুুতে ছেদ করেছে।
সুতরাং,
ক) ∠PEB = অনুরূপ ∠EFD [সংজ্ঞানুসারে]
খ) ∠AEF = একান্তর ∠EFD
গ) ∠BEF + ∠EFD = দুই সমকোণ বা 180°
0
Updated: 3 weeks ago
কোন ত্রিভুজের তিনটি বাহুকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণ তিনটির সমষ্টি কত?
Created: 1 month ago
A
২৭০°
B
১৮০°
C
৯০°
D
৩৬০°
প্রশ্ন: কোন ত্রিভুজের তিনটি বাহুকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণ তিনটির সমষ্টি কত?
সমাধান:
আমরা জানি, যেকোনো ত্রিভুজের তিনটি অন্তঃস্থ কোণের সমষ্টি ১৮০°।
যদি একটি ত্রিভুজের তিনটি অন্তঃস্থ কোণ যথাক্রমে A, B এবং C হয়, তবে,
A + B + C = ১৮০°
একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয়, তা তার অন্তঃস্থ সন্নিহিত কোণের সাথে ১৮০° কোণ তৈরি করে।
সুতরাং, বহিঃস্থ কোণ = ১৮০° - অন্তঃস্থ কোণ।
সকল বহিঃস্থ কোণের সমষ্টি = ৩ × ১৮০° - (A + B + C)
= ৫৪০° - ১৮০° = ৩৬০°
∴ যেকোনো ত্রিভুজের তিনটি বাহুকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণ তিনটির সমষ্টি সর্বদা ৩৬০°।
0
Updated: 1 month ago
একটি সরলরেখার সাথে আর একটি রশ্মির প্রান্তবিন্দু মিলিত হয়ে যে দুইটি সন্নিহিত কোণ উৎপন্ন হয় তাদের সমষ্টি কত হবে?
Created: 2 months ago
A
৯০°
B
১২০°
C
১৮০°
D
২৭০°
প্রশ্ন: একটি সরলরেখার সাথে আর একটি রশ্মির প্রান্তবিন্দু মিলিত হয়ে যে দুইটি সন্নিহিত কোণ উৎপন্ন হয় তাদের সমষ্টি কত হবে?
সমাধান:
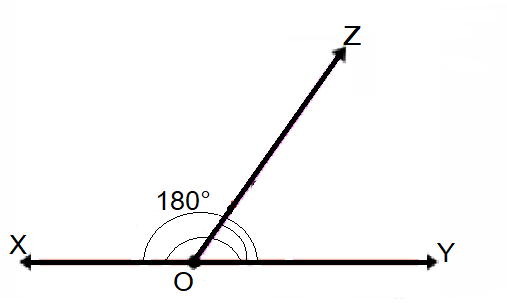
XY সরলরেখার সাথে OZ রশ্মির প্রান্তবিন্দু মিলিত হয়ে ∠XOZ ও ∠YOZ দুটি সন্নিহিত কোণ উৎপন্ন হয় এবং এদের সমষ্টি হবে এক সরলকোণ বা ১৮০ ডিগ্রি।
∴ ∠XOZ + ∠YOZ = ১৮০°
0
Updated: 2 months ago