A man takes twice as long to row a distance against the stream as to row the same distance in favour of the stream. The ratio of the speed of the boat (in still water) and the stream is:
A
3 : 1
B
3 : 2
C
7 : 2
D
5 : 3
উত্তরের বিবরণ
Question: A man takes twice as long to row a distance against the stream as to row the same distance in favour of the stream. The ratio of the speed of the boat (in still water) and the stream is:
Solution:
Let man's rate upstream be x kmph.
Then, his rate downstream = 2x kmph.
∴ (Speed in still water) : (Speed of stream) = {(2x + x)/2} : {(2x - x)/2}
= (3x/2) : (x/2)
= 3 : 1
0
Updated: 1 month ago
এক ব্যক্তি কোন স্থান থেকে যাত্রা শুরু করে দক্ষিণ দিকে 10 কি.মি. গেল। আবার সে পূর্ব দিকে 5 কি.মি.গেলো এবং গতি পরিবর্তন করে পুনরায় দক্ষিণ দিকে 7 কি.মি. গেলো এবং শেষে পশ্চিম দিকে 5কি.মি. গেলো। তার গন্তব্য স্থান ও যাত্রা স্থানের সরাসরি দূরত্ব কত?
Created: 1 month ago
A
20 কি.মি.
B
12 কি.মি.
C
14 কি.মি.
D
17 কি.মি.
প্রশ্ন: এক ব্যক্তি কোন স্থান থেকে যাত্রা শুরু করে দক্ষিণ দিকে 10 কি.মি. গেল। আবার সে পূর্ব দিকে 5 কি.মি.গেলো এবং গতি পরিবর্তন করে পুনরায় দক্ষিণ দিকে 7 কি.মি. গেলো এবং শেষে পশ্চিম দিকে 5কি.মি. গেলো। তার গন্তব্য স্থান ও যাত্রা স্থানের সরাসরি দূরত্ব কত?
সমাধান: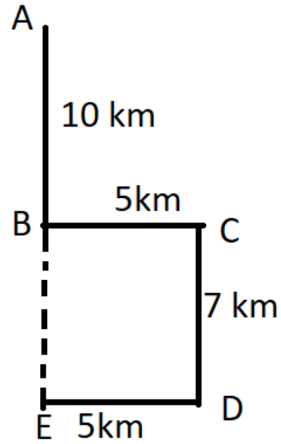
যাত্রাস্থান A এবং গন্তব্য স্থান E
সরাসরি দূরত্ব AE = (10 + 7) কি.মি. = 17 কি.মি.
0
Updated: 1 month ago
লিভারের ভারসাম্য বজায় রাখতে চিহ্নিত প্রশ্নবোধক স্থানের দূরত্ব কত হওয়া উচিত?
Created: 1 month ago
A
5 ফুট
B
6 ফুট
C
9 ফুট
D
10 ফুট
মানসিক দক্ষতা
মানসিক দক্ষতা (Mental skills)
সময়, দূরত্ব ও গতিবেগ (Time, distance & speed)
সীমা চিহ্নিতকরণ রেখা ও অক্ষরেখা
প্রশ্ন: লিভারের ভারসাম্য বজায় রাখতে চিহ্নিত প্রশ্নবোধক স্থানের দূরত্ব কত হওয়া উচিত?
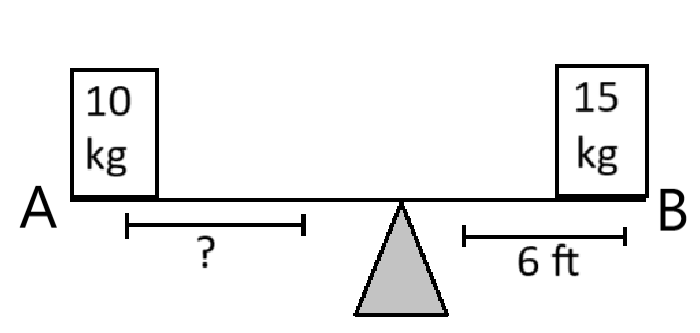
সমাধান:
ধরি,
A প্রান্ত ও ফালক্রামের মধ্যবর্তী দূরত্ব = x ফুট
প্রশ্নমতে,
10x = 15 × 6
⇒ 10x = 90
⇒ x = 90/10
⇒ x = 9
0
Updated: 1 month ago
Rahman is a boatman. He can row a boat at the speed of 5 km/hr upstream and 15 km/hr downstream. Find the speed of the stream.
Created: 1 month ago
A
5 km/hr
B
8 km/hr
C
6 km/hr
D
4 km/hr
Question: Rahman is a boatman. He can row a boat at the speed of 5 km/hr upstream and 15 km/hr downstream. Find the speed of the stream.
Solution:
Let’s denote:
B as Speed of the boat in still water (km/h)
S as Speed of the stream (km/h)
Speed of the boat upstream is the speed of the boat in still water minus the speed of the stream:
B - S = 5 km/hr -------- (1)
Speed of the boat downstream is the speed of the boat in still water plus the speed of the stream:
B + S = 15 km/hr -------- (2)
(1) + (2)
B - S = 5
B + S = 15
2B = 20
∴ B = 10 km/hr
Putting the value of B in (2)
∴ S = (15 - 10) km/hr = 5 km/hr
∴ The speed of the stream is 5 km/hr
0
Updated: 1 month ago