বার্ষিক শতকরা 10 টাকা মুনাফায় 5000 টাকার 3 বছরের সরল মুনাফা ও চক্রবৃদ্ধি মুনাফার পার্থক্য কত হবে?
A
150 টাকা
B
155 টাকা
C
165 টাকা
D
185 টাকা
উত্তরের বিবরণ
প্রশ্ন: বার্ষিক শতকরা 10 টাকা মুনাফায় 5000 টাকার 3 বছরের সরল মুনাফা ও চক্রবৃদ্ধি মুনাফার পার্থক্য কত হবে?
সমাধান:
দেওয়া আছে,
আসল, p = 5000 টাকা
সময়, n = 3 বছর
মুনাফার হার, r = 10%
আমরা জানি,
চক্রবৃদ্ধি মুনাফা
= p(1 + r)n - p
= 5000 × {1 + (10/100)}3 - 5000
= 5000 × {1 + (1/10)}3 - 5000
= 5000 × {(10 + 1)/10}3 - 5000
= 5000 × (11/10)3 - 5000
= 5000 × {(1331/1000) - 1}
= 5000 × {(1331 - 1000)/1000}
= 5000 × (331/1000)
= 1655
এবং , সরল মুনাফা
= pnr/১০০
= (5000 × 3 × 10)/100
= 500 × 3
=1500
∴ পার্থক্য = চক্রবৃদ্ধি মুনাফা - সরল মুনাফা
= 1655 - 1500
= 155
0
Updated: 1 month ago
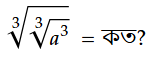
Created: 2 months ago
A
a
B
1
C
a1/3
D
a3
প্রশ্ন: 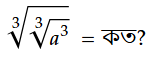
সমাধান:
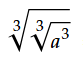
= {(a3)1/3}1/3
= a1/3
0
Updated: 2 months ago
4x + 41 - x = 4 হলে, x = কত?
Created: 1 month ago
A
1/4
B
1/3
C
1/2
D
1
প্রশ্ন: 4x + 41 - x = 4 হলে, x = কত?
সমাধান:
4x + 41 - x = 4
⇒ 4x + 41/4x = 4
⇒ 4x + 4/4x = 4 [41 = 4]
মনে করি, 4x = y
সুতরাং,
y + 4/y = 4
বা, (y2 + 4)/y = 4
বা, y2 + 4 = 4y
বা, y2 - 4y + 4 = 0
বা, y2 - 2.y.2 + 22 = 0
বা, (y - 2)2 = 0
বা, y - 2 = 0
বা, y = 2
বা, 4x = 2 [y = 4x বসিয়ে]
বা, (22)x = 21 [21 = 2]
বা, 22x = 21
বা, 2x = 1
∴ x = 1/2
0
Updated: 1 month ago
দুইটি সংখ্যার যোগফল এবং বিয়োগফল যথাক্রমে ৩২ এবং ৮। বড় সংখ্যাটি কত?
Created: 1 month ago
A
১২
B
১৬
C
২০
D
২৪
গণিত
অসমতা (Inequality)
বীজগণিত (Algebra)
সরল সমীকরণ (Simple/linear equation)
সরলীকরণ (Simplification)
প্রশ্ন: দুইটি সংখ্যার যোগফল এবং বিয়োগফল যথাক্রমে ৩২ এবং ৮। বড় সংখ্যাটি কত?
সমাধান:
ধরি,
বড় সংখ্যা = x
ছোট সংখ্যা = y
শর্তমতে,
x + y = ৩২ ...........(১)
x - y = ৮ ...............(২)
এখন, সমীকরণ দুটি যোগ করে পাই,
(x + y) + (x - y) = ৩২ + ৮
⇒ ২x = ৪০
⇒ x = ৪০/২
⇒ x = ২০
সুতরাং, বড় সংখ্যাটি হলো ২০।
0
Updated: 1 month ago