একটি সমকোণী ত্রিভুজে সমকোণ ছাড়া দুটি কোণের মধ্যে পার্থক্য ১০°। ঐ দুটি কোণের মধ্যে বৃহত্তম কোণটির মান কত?
A
৫০°
B
৬০°
C
৩০°
D
৯০°
উত্তরের বিবরণ
প্রশ্ন: একটি সমকোণী ত্রিভুজে সমকোণ ছাড়া দুটি কোণের মধ্যে পার্থক্য ১০°। ঐ দুটি কোণের মধ্যে বৃহত্তম কোণটির মান কত?
সমাধান:
ধরি,
অপর দুইটি কোণের মধ্যে ক্ষুদ্রতম কোণ = ক°
∴ বৃহত্তম কোণ = (ক + ১০)°
প্রশ্নমতে,
ক + (ক + ১০) + ৯০ = ১৮০
⇒ ২ক + ১০০ = ১৮০
⇒ ২ক = ১৮০ - ১০০
⇒ ২ক = ৮০
⇒ ক = ৮০/২
∴ ক = ৪০
∴ বৃহত্তম কোণ = (৪০ + ১০)°
= ৫০°
0
Updated: 1 month ago
একটি শ্রেণিতে ২৫ জন ছাত্রের মধ্যে ১২ জন জীববিজ্ঞান এবং ৭ জন জীববিজ্ঞান ও উচ্চতর গণিত উভয় বিষয় নিয়েছে। ২ জন ছাত্র কোনো বিষয় নেয়নি। কতজন ছাত্র শুধু উচ্চতর গণিত নিয়েছে?
Created: 1 month ago
A
১১ জন
B
১২ জন
C
৯ জন
D
১০ জন
কোনো বিষয় নেয়নি = ২ জন
উভয় বিষয় নিয়েছে = ৭ জন
শুধু জীববিজ্ঞান নিয়েছে = (১২ - ৭) জন = ৫ জন
ধরি,
শুধু উচ্চতর গণিত নিয়েছে = x জন
প্রশ্নমতে,
৫ + x + ৭ + ২ = ২৫
⇒ ১৪ + x = ২৫
⇒ x = ২৫ - ১৪
⇒ x = ১১
অর্থাৎ ১১ জন ছাত্র শুধু উচ্চতর গণিত নিয়েছে।
0
Updated: 1 month ago
একটি সমবাহু ত্রিভুজের ক্ষেত্রফল 36√3 বর্গমিটার হলে ত্রিভুজটির একটি বাহুর দৈর্ঘ্য কত?
Created: 2 months ago
A
6 মিটার
B
12 মিটার
C
6√3 মিটার
D
16 মিটার
প্রশ্ন: একটি সমবাহু ত্রিভুজের ক্ষেত্রফল 36√3 বর্গমিটার হলে ত্রিভুজটির একটি বাহুর দৈর্ঘ্য কত?
সমাধান:
দেওয়া আছে,
সমবাহু ত্রিভুজের ক্ষেত্রফল = 36√3 বর্গমিটার
আমরা জানি,
সমবাহু ত্রিভুজের ক্ষেত্রফল = (√3/4) × (বাহু)2
প্রশ্নমতে,
(√3/4) × (বাহু)2 = 36√3
⇒ (বাহু)2 = (36√3 × 4)/√3
⇒ (বাহু)2 = 144
⇒ বাহু = 12 [ বর্গমূল করে ]
0
Updated: 2 months ago
ΔABC সমবাহু ত্রিভুজের একটি মধ্যমা AD এবং G ভরকেন্দ্র। GD = ৫ সেমি হলে AD = ?
Created: 3 weeks ago
A
১৫ সেমি
B
১০ সেমি
C
৭.৫ সেমি
D
১২ সেমি
প্রশ্ন: ΔABC সমবাহু ত্রিভুজের একটি মধ্যমা AD এবং G ভরকেন্দ্র। GD = ৫ সেমি হলে AD = ?
সমাধান:
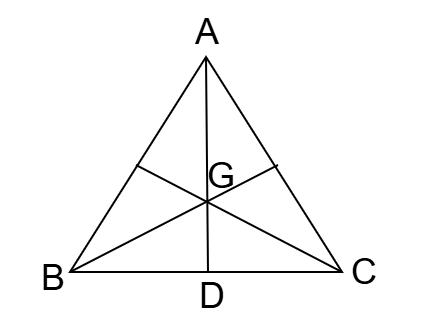
আমরা জানি,
ত্রিভুজের ভরকেন্দ্র (G) মধ্যমাকে (AD) ২ : ১ অনুপাতে বিভক্ত করে।
অর্থাৎ, AG : GD = ২ : ১
দেওয়া আছে, GD = ৫ সেমি।
প্রশ্নমতে,
AG : GD = ২ : ১
⇒ AG/৫ = ২/১
⇒ AG = ৫ × ২
∴ AG = ১০
এখন, মধ্যমা AD = AG + GD
= ১০ সেমি + ৫ সেমি
= ১৫ সেমি
0
Updated: 3 weeks ago