x2 - 3x - 10 > 0 অসমতাটির সমাধান কোনটি?
A
(-∞, -1) U (4, +∞)
B
(-∞, -2) U (5, +∞)
C
(∞, 2) U (5, +∞)
D
(-5, -∞) U (∞, 2)
উত্তরের বিবরণ
প্রশ্ন: x2 - 3x - 10 > 0 অসমতাটির সমাধান কোনটি?
সমাধান:
x2 - 3x - 10 > 0
⇒ x2 - 5x + 2x - 10 > 0
⇒ x(x - 5) + 2(x - 5) > 0
∴ (x - 5)(x + 2) > 0
দুইটি রাশির গুনফল তখনই ধনাত্মক বা শূন্য অপেক্ষা বড় হবে যদি উভয়ই ধনাত্মক অথবা উভয়েই ঋণাত্মক হয়।
∴ নির্ণেয় সমাধান = (- ∞, - 2) ∪ (5, + ∞)
0
Updated: 1 month ago
(2x-3y)/(2x+3y) = 1/7 হলে x:y = কত?
Created: 1 day ago
A
2:3
B
3:2
C
2:1
D
1:2
প্রশ্নঃ (2x−3y)/(2x+3y) = 1/7 হলে x : y = কত?
সমাধানঃ
প্রদত্ত,
(2x−3y)/(2x+3y) = 1/7
অতএব,
7(2x−3y) = 1(2x+3y)
⇒ 14x − 21y = 2x + 3y
⇒ 14x − 2x = 3y + 21y
⇒ 12x = 24y
⇒ x/y = 24/12
⇒ x/y = 2/1
অতএব, x : y = 2 : 1
উত্তরঃ গ) 2 : 1
0
Updated: 1 day ago
একটি ত্রিভুজাকৃতি জমির ভূমি ৬০ মিটার এবং উচ্চতা ১৫ মিটার। প্রতি বর্গমিটারে ২.০০ টাকা হিসেবে ঘাস লাগাতে কত টাকা খরচ হবে?
Created: 1 month ago
A
৮০০ টাকা
B
৭০০ টাকা
C
৯০০ টাকা
D
৬০০ টাকা
প্রশ্ন: একটি ত্রিভুজাকৃতি জমির ভূমি ৬০ মিটার এবং উচ্চতা ১৫ মিটার। প্রতি বর্গমিটারে ২.০০ টাকা হিসেবে ঘাস লাগাতে কত টাকা খরচ হবে?
সমাধান:
দেওয়া আছে,
ত্রিভুজাকৃতি জমির ভূমি = ৬০ মিটার
ত্রিভুজাকৃতি জমির উচ্চতা = ১৫ মিটার
∴ ত্রিভুজাকৃতি জমির ক্ষেত্রফল = (১/২) × (ভূমি × উচ্চতা) বর্গমিটার
= (১/২) × (৬০ × ১৫) বর্গমিটার
= ৪৫০ বর্গমিটার
১ বর্গমিটারে খরচ হয় = ২ টাকা
∴ ৪৫০ বর্গমিটারে খরচ হয় = (২ × ৪৫০) টাকা
= ৯০০ টাকা
∴ ঘাস লাগাতে খরচ হবে = ৯০০ টাকা।
0
Updated: 1 month ago
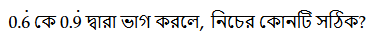
Created: 1 month ago
A
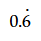
B
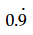
C
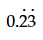
D
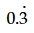
প্রশ্ন:
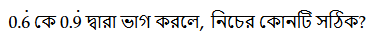
সমাধান:
সঠিক উত্তর: ক
0
Updated: 1 month ago