একটি পিকনিকে যতজন বন্ধু ছিল, প্রত্যেকে তার থেকে 4 টাকা বেশি করে দেওয়ায় মোট 320 টাকা উঠল। পিকনিকে বন্ধুর সংখ্যা কত ছিল?
A
18 জন
B
16 জন
C
20 জন
D
12 জন
উত্তরের বিবরণ
প্রশ্ন: একটি পিকনিকে যতজন বন্ধু ছিল, প্রত্যেকে তার থেকে 4 টাকা বেশি করে দেওয়ায় মোট 320 টাকা উঠল। পিকনিকে বন্ধুর সংখ্যা কত ছিল?
সমাধান:
মনে করি, পিকনিকে বন্ধুর সংখ্যা = x জন
প্রত্যেকে চাঁদা দেয় = (x + 4) টাকা
প্রশ্নমতে,
⇒ x(x + 4) = 320
⇒ x2 + 4x = 320
⇒ x2 + 4x - 320 = 0
⇒ x2 + 20x - 16x - 320 = 0
⇒ x(x + 20) - 16(x + 20) = 0
⇒ (x - 16)(x + 20) = 0
হয়, x - 16 = 0
⇒ x = 16
অথবা, x + 20 = 0
⇒ x = - 20 (বন্ধুর সংখ্যা ঋণাত্মক হতে পারে না, তাই এটি গ্রহণযোগ্য নয়)
∴ পিকনিকে বন্ধুর সংখ্যা 16 জন ছিল।
0
Updated: 1 month ago
৫ + ৯ + ১৩ + ১৭ + ...... ধারার কোন পদ ১৭৩?
Created: 1 month ago
A
৩৭
B
৪৩
C
৪৭
D
৫১
প্রশ্ন: ৫ + ৯ + ১৩ + ১৭ + ...... ধারার কোন পদ ১৭৩?
সমাধান:
প্রথম পদ, a = ৫
সাধারণ অন্তর, d = ৯ - ৫ = ৪
n তম পদ = ১৭৩
আমরা জানি,
n তম পদ = a + (n - ১) × d
⇒ ১৭৩ = ৫ + (n - ১) × ৪
⇒ ১৭৩ = ৫ + ৪n - ৪
⇒ ১৭৩ = ৪n + ১
⇒ ৪n = ১৭২
⇒ n = ১৭২/৪
∴ n = ৪৩
∴ ধারাটির ৪৩তম পদ হলো ১৭৩
0
Updated: 1 month ago
(xa/xb)(a + b) (xb/xc)(b + c) (xc/xa)(c + a) এর মান কত?
Created: 2 months ago
A
0
B
1
C
- 1
D
1/2
প্রশ্ন: (xa/xb)(a + b) (xb/xc)(b + c) (xc/xa)(c + a) এর মান কত?
সমাধান: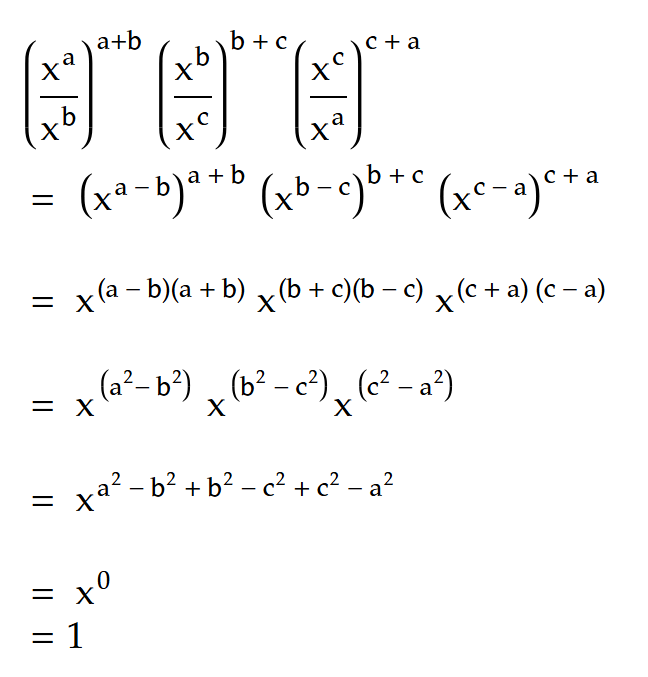
0
Updated: 2 months ago
a + b = √5 এবং a - b = √3 হলে, 8ab(a2 + b2) = ?
Created: 2 months ago
A
12
B
16
C
36
D
42
গণিত
বীজগণিত (Algebra)
বীজগণিতীয় রাশিমালার যোগ, বিয়োগ, গুণ ও ভাগ (Addition, subtraction, multiplication and division of algebraic expressions)
প্রশ্ন: a + b = √5 এবং a - b = √3 হলে, 8ab(a2 + b2) = ?
সমাধান:
দেওয়া আছে,
a + b = √5 এবং a - b = √3
এখন,
8ab(a2 + b2)
= 4ab × 2(a2 + b2)
= {(a + b)2 - (a - b)2}{(a + b)2 + (a - b)2}
= {(√5)2 - (√3)2}{(√5)2 +(√3)2}
= (5 - 3)(5 + 3)
= 2 × 8
= 16
0
Updated: 2 months ago