প্রশ্ন: একটি ট্রেন ঘণ্টায় ৪৫ কিলোমিটার গতিতে একটি সেতু ৫০ সেকেন্ডে পার হলো। ট্রেনের দৈর্ঘ্য ২৫০ মিটার হলে সেতুটির দৈর্ঘ্য কত মিটার?

সমাধান: 

এখানে, 

৪৫ কিলোমিটার = (৪৫ × ১০০০) মিটার  

= ৪৫০০০ মিটার

আমনা জানি,

১ ঘণ্টা = ৩৬০০ মিনিট

৩৬০০ সেকেন্ডে ট্রেনটি অতিক্রম করে = ৪৫০০০ মিটার

∴ ৫০ সেকেন্ডে ট্রেনটি অতিক্রম করে = (৪৫০০০ × ৫০)/৩৬০০ = ৬২৫ মিটার

 আমরা জানি,

সেতু অতিক্রম করার জন্য ট্রেনকে তার নিজের দৈর্ঘ্য ও সেতুর দৈর্ঘ্যের সমান পথ অতিক্রম করতে হবে।

∴ সেতুটির দৈর্ঘ্য = (৬২৫ - ২৫০) মিটার

= ৩৭৫ মিটার

প্রশ্ন: 18 মিটার দীর্ঘ একটি মই ভূমির সাথে 45° কোণে হেলান দিয়ে একটি দেয়ালের ছাদ স্পর্শ করে। দেয়ালটির উচ্চতা কত?

সমাধান: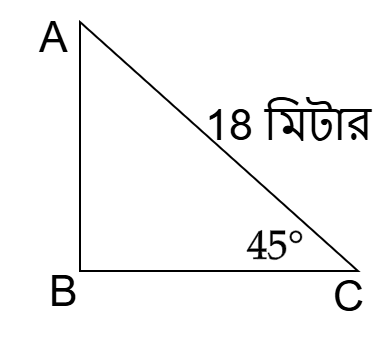

এখানে, মইটির দৈর্ঘ্য (অতিভুজ), AC = 18 মিটার।
ভূমির সাথে উৎপন্ন কোণ, ∠ACB = 45°
দেয়ালের উচ্চতা (লম্ব), AB = ?

আমরা জানি,
sinθ = লম্ব/অতিভুজ
বা, sin45° = AB/AC
বা, 1/√2 = AB/18
বা, √2AB = 18
বা, AB = 18/√2
বা, AB = (18 × √2)/(√2 × √2)
বা, AB = (18√2)/2
∴ AB = 9√2 মিটার

সুতরাং, দেয়ালটির উচ্চতা 9√2 মিটার।

প্রশ্ন: একটি 15 মিটার লম্বা মই দেয়ালের সাথে খাড়া করে রাখা আছে। মইটির গোড়া দেয়াল থেকে কত দূরে সরালে এর উপরের অংশ 6 মিটার নিচে নেমে আসবে?

সমাধান: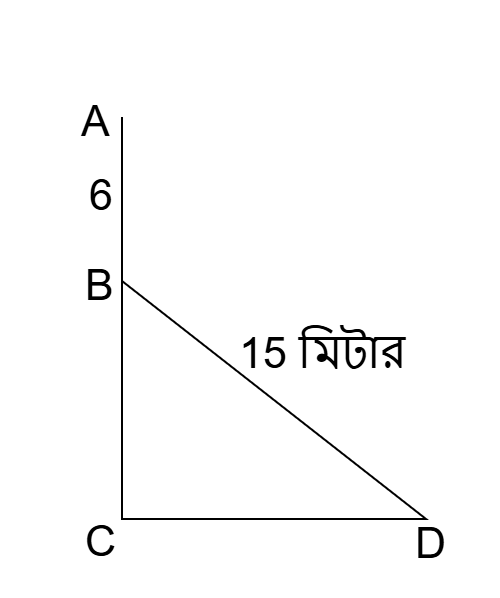

এখানে,
AC মইয়ের গোড়া C থেকে D বিন্দুতে সরালে উপরের প্রান্ত 
A বিন্দু থেকে B বিন্দুতে 6 মিটার নামবে।
মইয়ের দৈর্ঘ্য, AC = BD = 15 মিটার।
দেয়ালের উচ্চতা যেখানে মইটি প্রথমে ছিল (AC) = 15 মিটার।
এবং AB = 4 মিটার
BC = 15 - 6 = 9 মিটার

এখন, 
পিথাগোরাসের সূত্র অনুযায়ী,
BC2 + CD2 = BD2
বা, 92 + CD2 = 152
বা, 81 + CD2 = 225
বা, CD2 = 225 - 81
বা, CD2 = 144
বা, CD = √144
বা, CD = 12 মিটার।

সুতরাং, মইটির গোড়া দেয়াল থেকে 12 মিটার দূরে সরাতে হবে।