P, Q, and R are three consecutive even integers. If P + R = Q + 14, what is the value of P?
A
10
B
8
C
14
D
12
উত্তরের বিবরণ
Question: P, Q, and R are three consecutive even integers. If P + R = Q + 14, what is the value of P?
Solution:
ধরি, P, Q, এবং R হলো তিনটি ক্রমিক জোড় পূর্ণসংখ্যা। যেখানে,
P = n (জোড় পূর্ণসংখ্যা)
Q = n + 2 (পরবর্তী ক্রমিক জোড় পূর্ণসংখ্যা)
R = n + 4 (তৃতীয় ক্রমিক জোড় পূর্ণসংখ্যা)
দেয়া আছে,
P + R = Q + 14
⇒ n + (n + 4) = (n + 2) + 14
⇒ 2n + 4 = n + 16
⇒ 2n - n = 16 - 4
∴ n = 12
অতএব, P = 12, Q = 14, R = 16
সুতরাং, P এর মান হলো 12.
0
Updated: 1 month ago
একটি গুণোত্তর ধারার চতুর্থ পদ 162 এবং ষষ্ঠ পদ 1458 হলে, ধারাটির সাধারণ অনুপাত কত?
Created: 1 month ago
A
3
B
5
C
4
D
7
প্রশ্ন: একটি গুণোত্তর ধারার চতুর্থ পদ 162 এবং ষষ্ঠ পদ 1458 হলে, ধারাটির সাধারণ অনুপাত কত?
সমাধান:
ধরি,
প্রথম পদ = a
সাধারণ অনুপাত = r
আমরা জানি,
গুণোত্তর ধারার n তম পদ = a × rn - 1
চতুর্থ পদ = ar4 - 1 = ar3 = 162 ........(1)
ষষ্ঠ পদ = ar6 - 1 = ar5 = 1458 .........(2)
(2) ÷ (1) করলে পাই,
(ar5)/(ar3) = 1458/162
⇒ r5 - 3 = 9
⇒ r2 = 32
⇒ r = 3
∴ ধারাটির সাধারণ অনুপাত = ৩
0
Updated: 1 month ago
একটি মোটর সাইকেল ১২% ক্ষতিতে বিক্রি করা হলো। যদি বিক্রয়মূল্য ১২০০ টাকা বেশি হতো, তাহলে ৮% লাভ হতো। মোটর সাইকেলের ক্রয়মূল্য -
Created: 1 month ago
A
৬০০০ টাকা
B
৫০০০ টাকা
C
৪০০০ টাকা
D
৮০০০ টাকা
প্রশ্ন: একটি মোটর সাইকেল ১২% ক্ষতিতে বিক্রি করা হলো। যদি বিক্রয়মূল্য ১২০০ টাকা বেশি হতো, তাহলে ৮% লাভ হতো। মোটর সাইকেলের ক্রয়মূল্য -
সমাধান:
১২% ক্ষতিতে,
ক্রয়মূল্য ১০০ টাকা হলে বিক্রয় মূল্য = (১০০ - ১২) = ৮৮ টাকা
৮% লাভে,
বিক্রয়মূল্য = (১০০ + ৮) = ১০৮ টাকা।
∴ বিক্রয়মূল্যেদ্বয়ের পার্থক্য = (১০৮ - ৮৮) = ২০ টাকা।
বিক্রয় মূল্য ২০ টাকা বেশি হলে ক্রয় মূল্য ১০০ টাকা
বিক্রয় মূল্য ১ টাকা বেশি হলে ক্রয় মূল্য ১০০/২০ টাকা
∴ বিক্রয় মূল্য ১২০০ টাকা বেশি হলে ক্রয় মূল্য (১০০ × ১২০০)/২০
= ৬০০০ টাকা।
0
Updated: 1 month ago
চিত্রে ∠PQR = 55°, ∠LRN = 90° এবং PQ || MR, PQ = PR হলে, ∠NRP এর মান নিচের কোনটি?
Created: 1 month ago
A
90°
B
55°
C
45°
D
35°
প্রশ্ন: চিত্রে ∠PQR = 55°, ∠LRN = 90° এবং PQ || MR, PQ = PR হলে, ∠NRP এর মান নিচের কোনটি?
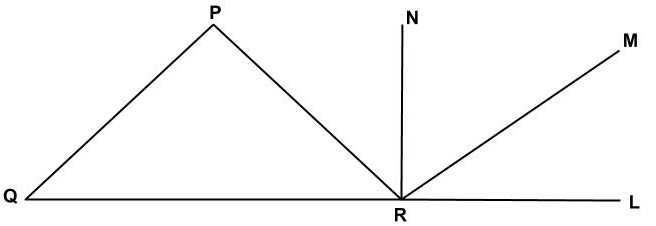
সমাধান:
প্রদত্ত চিত্রে,
PQ = PR
সুতরাং, PQR সমদ্বিবাহু ত্রিভুজ।
∠PQR = ∠PRQ = 55°
∠LRN = 90° হলে ∠NRQ = 90°
সুতরাং, ∠NRP = ∠NRQ - ∠PRQ = 90° - 55° = 35°
0
Updated: 1 month ago