ΔABC এর ∠A = 40° এবং ∠B = 80°। ∠C এর সমদ্বিখণ্ডক AB বাহুকে D বিন্দুতে ছেদ করলে ∠CDA = ?
A
110°
B
100°
C
90°
D
80°
উত্তরের বিবরণ
প্রশ্ন: ΔABC এর ∠A = 40° এবং ∠B = 80°। ∠C এর সমদ্বিখণ্ডক AB বাহুকে D বিন্দুতে ছেদ করলে ∠CDA = ?
সমাধান:
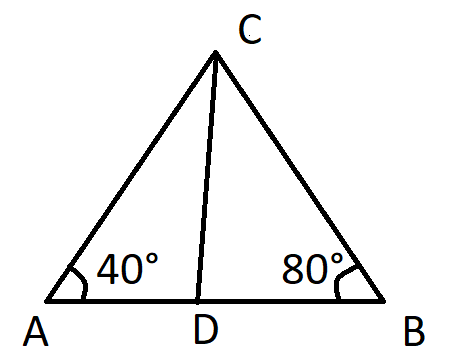
ΔABC এর ∠A = 40° এবং ∠B = 80°।
∠C = 180° - 40° - 80°
= 60°
∠C এর সমদ্বিখণ্ডক CD, AB বাহুকে D বিন্দুতে ছেদ করে।
∴ ∠ACD = ∠BCD = 30°
∴ ∠CDA = 180° - 30° - 40°
= 110°
0
Updated: 1 month ago
১৮° কোণের বিপ্রতীপ কোণের মান কত?
Created: 2 months ago
A
১৮°
B
৭২°
C
১০২°
D
১৬২°
সমাধান:
আমরা জানি,
বিপ্রতীপ কোণদ্বয় পরস্পর সমান হয়।
তাই ১৮° কোণের বিপ্রতীপ কোণের মানও হবে ১৮° অর্থাৎ সমান।
0
Updated: 2 months ago
দুটি সন্নিহিত কোণের সমষ্টি দুই সমকোণ হলে একটিকে অপরটির কি বলে?
Created: 2 months ago
A
সন্নিহিত কোণ
B
সরলকোণ
C
পূরককোণ
D
সম্পূরক কোণ
প্রশ্ন: দুটি সন্নিহিত কোণের সমষ্টি দুই সমকোণ হলে একটিকে অপরটির কি বলে?
সমাধান:
- দুটি সন্নিহিত কোণের সমষ্টি দুই সমকোণ বা ১৮০° হলে একটিকে অপরটির সম্পূরক কোণ বলে।
- দুটি সন্নিহিত কোণের সমষ্টি এক সমকোণ বা ৯০° হলে একটিকে অপরটির পূরক কোণ বলে।
- দুটি কোণের একই শীর্ষবিন্দু এবং একটি সাধারণ বাহু থাকলে কোণ দুইটির একটিকে অপরটির সন্নিহিত কোণ করে।
0
Updated: 2 months ago
একটি সমদ্বিবাহু ত্রিভুজের পরিসীমা ১৮ মিটার। এর সমান সমান বাহুর দৈর্ঘ্য ভূমির ৫/৮ অংশ হলে, ত্রিভুজটির ক্ষেত্রফল কত?
Created: 1 month ago
A
১২ বর্গমিটার
B
১৬ বর্গমিটার
C
২৫ বর্গমিটার
D
৩৪ বর্গমিটার
প্রশ্ন: একটি সমদ্বিবাহু ত্রিভুজের পরিসীমা ১৮ মিটার। এর সমান সমান বাহুর দৈর্ঘ্য ভূমির ৫/৮ অংশ হলে, ত্রিভুজটির ক্ষেত্রফল কত?
সমাধান:
ধরি, ত্রিভুজটির ভূমি, b = ক মিটার
∴ ত্রিভুজটির সমান সমান বাহুর দৈর্ঘ্য a = (৫/৮)ক মিটার
প্রশ্নমতে,
ক + (৫/৮)ক + (৫/৮)ক = ১৮
⇒ (৮ক + ৫ক + ৫ক)/৮ = ১৮
⇒ ৯ক/৪ = ১৮
⇒ ৯ক = ১৮ × ৪
⇒ ৯ক = ৭২
⇒ ক = ৭২/৯
⇒ ক = ৮
∴ ত্রিভুজটির ভূমি b = ৮ মিটার
এবং সমান সমান বাহুর দৈর্ঘ্য a = (৫/৮) × ৮ = ৫ মিটার
এখন, ত্রিভুজটির ক্ষেত্রফল = (b/৪) × √(৪a২ - b২)
= (৮/৪) × √{৪(৫)২ - (৮)২}
= ২ × √(৪ × ২৫ - ৬৪)
= ২ × √(১০০ - ৬৪)
= ২ × √৩৬
= ২ × ৬
= ১২ বর্গমিটার
∴ ত্রিভুজটির ক্ষেত্রফল ১২ বর্গমিটার।
0
Updated: 1 month ago