(- 4, 5) এবং (1, 2) বিন্দুগামী একটি সরলরেখার ঢাল কত?
A
3/5
B
7/3
C
- 5/3
D
- 3/5
উত্তরের বিবরণ
প্রশ্ন: (- 4, 5) এবং (1, 2) বিন্দুগামী একটি সরলরেখার ঢাল কত?
সমাধান:
আমরা জানি,
দুটি বিন্দু (x1, y1) এবং (x2, y2) দিয়ে অতিক্রমকারী একটি সরলরেখার ঢাল (m) নির্ণয়ের সূত্র হলো:
m = (y2 - y1)/(x2 - x1)
এখানে,
(x1, y1) = (- 4, 5) এবং (x2, y2) = (1, 2)
∴ ঢাল, (m) = (2 - 5)/{1 - (- 4)}
= - 3/(1 + 4)
= - 3/5
0
Updated: 1 month ago
সূর্যের উন্নতি কোণ 60° হলে একটি মিনারের ছায়ার দৈর্ঘ্য 240 মিটার হয়। মিনারটির উচ্চতা কত?
Created: 1 month ago
A
418.45 মি.
B
319.69 মি.
C
415.69 মি.
D
315.69 মি.
প্রশ্ন: সূর্যের উন্নতি কোণ 60° হলে একটি মিনারের ছায়ার দৈর্ঘ্য 240 মিটার হয়। মিনারটির উচ্চতা কত?
সমাধান:
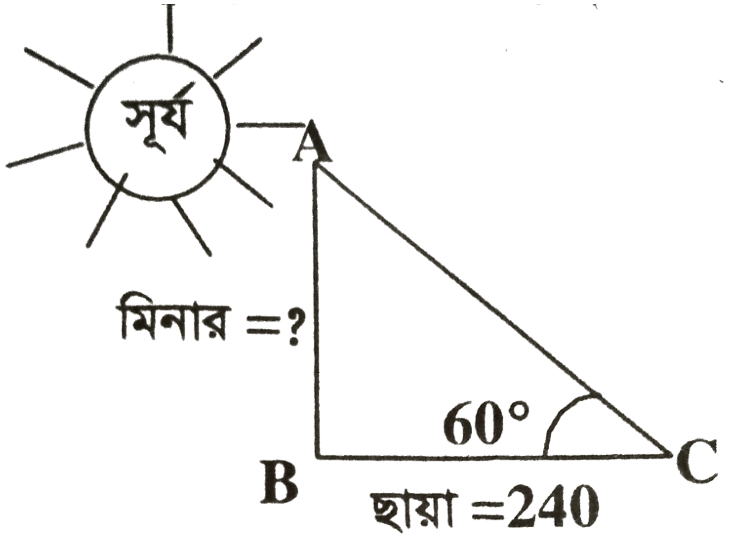
দেওয়া আছে,
মিনারের ছায়ার দৈর্ঘ্য, BC = 240 মিটার
সূর্যের উন্নতি কোণ, θ = 60°
মিনারটির উচ্চতা, AB (h) =?
চিত্র হতে পাই,
tanθ = AB/BC
বা, tan60° = AB/240
বা, √3 = AB/240
বা, AB = 240 × √3
∴ AB = 415.69 মিটার
∴ মিনারটির উচ্চতা = 415.69 মিটার।
0
Updated: 1 month ago
যদি tanθ = 3/4 হয়, তবে sinθ এর মান কত?
Created: 3 weeks ago
A
4/5
B
5/4
C
4/3
D
3/5
প্রশ্ন: যদি tanθ = 3/4 হয়, তবে sinθ এর মান কত?
সমাধান:
দেওয়া আছে, tanθ = 3/4
আমরা জানি,
সমকোণী ত্রিভুজে, tanθ = লম্ব/ভূমি।
অতএব, লম্ব = 3 এবং ভূমি = 4।
এখন,
অতিভুজ2 = লম্ব2 + ভূমি2
বা, অতিভুজ = √(লম্ব2 + ভূমি2)
বা, অতিভুজ = √(32 + 42)
বা, অতিভুজ = √(9 + 16)
বা, অতিভুজ = √25
∴ অতিভুজ = 5
আমরা জানি,
sinθ = লম্ব/অতিভুজ
∴ sinθ = 3/5
0
Updated: 3 weeks ago
sin(P + 18°) = 1/√2 হলে, P এর মান কত?
Created: 1 month ago
A
54°
B
42°
C
78°
D
27°
সমাধান:
দেওয়া আছে,
sin (P + 18°) = 1/√2
বা, sin (P + 18°) = sin 45°
বা, P + 18° = 45°
বা, P = 45° - 18°
∴ P = 27°
0
Updated: 1 month ago