যদি p + q = √7 এবং p - q = √3 হয়, তবে 8pq(p2 + q2) এর মান কত?
A
24
B
40
C
60
D
84
উত্তরের বিবরণ
সমাধান:
দেওয়া আছে,
p + q = √7
p - q = √3
আমরা জানি,
4pq = (p + q)2 - (p - q)2
এবং,
2(p2 + q2) = (p + q)2 + (p - q)2
এখন,
8pq(p2 + q2)
= (4pq) × 2(p2 + q2)
= [(p + q)2 - (p - q)2] × [(p + q)2 + (p - q)2]
= [(√7)2 - (√3)2] × [(√7)2 + (√3)2]
= (7 - 3) × (7 + 3)
= 4 × 10
= 40
সুতরাং, 8pq(p2 + q2) এর মান 40।
0
Updated: 1 month ago
125 এর 5 ভিত্তিক লগ কত ?
Created: 1 month ago
A
3
B
2√3
C
4
D
3√2
প্রশ্ন: 125 এর 5 ভিত্তিক লগ কত ?
সমাধান:
log5125
= log553
= 3 log55
= 3 × 1 [logaa = 1 ]
= 3
0
Updated: 1 month ago
হলে, x এর মান কত?
Created: 1 month ago
A
4
B
12
C
18
D
30
প্রশ্ন: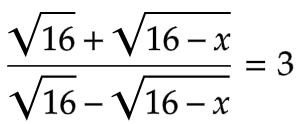 
হলে, x এর মান কত?
সমাধান:
0
Updated: 1 month ago
নিচের কোনটি (a3 + 8) ও (3a2 + a - 10) এর একটি সাধারণ উৎপাদক?
Created: 1 month ago
A
a + 2
B
a + 5
C
a + 4
D
a + 3
প্রশ্ন: নিচের কোনটি (a3 + 8) ও (3a2 + a - 10) এর একটি সাধারণ উৎপাদক?
সমাধান:
১ম রাশি = (a3 + 8)
= (a)3 + (2)3
= (a + 2){(a)2 - a · 2 + (2)2}
= (a + 2)(a2 - 2a + 4)
২য় রাশি = 3a2 + a - 10
= 3a2 + 6a - 5a - 10
= 3a(a + 2) - 5(a + 2)
= (a + 2)(3a - 5)
সুতরাং, প্রদত্ত রাশিদ্বয়ের সাধারণ উৎপাদক = a + 2
0
Updated: 1 month ago
