প্রশ্ন: একটি বর্গক্ষেত্রের ক্ষেত্রফল একটি সামান্তরিক ক্ষেত্রের ক্ষেত্রফলের সমান। বর্গক্ষেত্রের পরিসীমা ৫৬ মিটার এবং সামান্তরিকের উচ্চতা ৭ মিটার হলে, সামান্তরিকের ভূমি কত?

সমাধান:
দেওয়া আছে,
বর্গক্ষেত্রের পরিসীমা ৫৬ মিটার
বর্গক্ষেত্রের এক বাহুর দৈর্ঘ্য = ৫৬/৪ = ১৪ মিটার
বর্গক্ষেত্রের ক্ষেত্রফল = (বাহু)২ = (১৪)২
= ১৯৬ বর্গমিটার

এখন,
একটি বর্গক্ষেত্রের ক্ষেত্রফল একটি সামান্তরিক ক্ষেত্রের ক্ষেত্রফলের সমান।
∴ সামান্তরিকের ক্ষেত্রফল = ১৯৬ বর্গমিটার
সামান্তরিকের উচ্চতা = ৭ মিটার

∴ সামান্তরিকের ভূমি = ক্ষেত্রফল/উচ্চতা = ১৯৬/৭
= ২৮ মিটার

প্রশ্ন: একটি ২৫ মিটার লম্বা মই দেয়ালের সাথে হেলান দিয়ে রাখা হয়েছে। মইয়ের এক প্রান্ত দেয়াল থেকে ৭ মিটার দূরে থাকলে, মইয়ের অপর প্রান্ত দেয়ালের কত উচ্চতায় স্পর্শ করেছে?

সমাধান:
ধরি,
মইয়ের অপর প্রান্ত দেয়ালের "ক" মিটার উচ্চতায় স্পর্শ করেছে।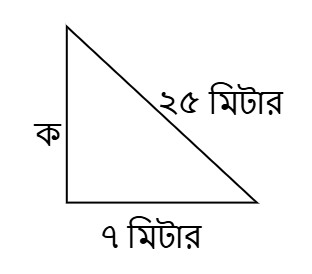

দেওয়া আছে,
মইয়ের দৈর্ঘ্য = ২৫ মিটার
দেয়াল থেকে মইয়ের দূরত্ব = ৭ মিটার

যেহেতু দেয়াল মাটির সাথে ৯০° কোণ উৎপন্ন করে।

∴ পিথাগোরাসের সূত্রানুসারে,
(দেয়ালের উচ্চতা)২ + (৭)২ = (২৫)২
⇒ (দেয়ালের উচ্চতা)২ + ৪৯ = ৬২৫
⇒ (দেয়ালের উচ্চতা)২ = ৬২৫ - ৪৯ = ৫৭৬
⇒ দেয়ালের উচ্চতা = √৫৭৬ = ২৪

সুতরাং, মইয়ের অপর প্রান্ত দেয়ালের ২৪ মিটার উচ্চতায় স্পর্শ করেছে।

প্রশ্ন:

​
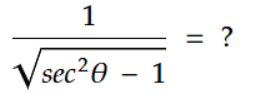
​সমাধান:
​