যদি f(x) = 2x - 5 এবং g(x) = x2 + 6 হয় তবে g(f(x)) - 1 এর মান হবে কত?
A
4x2 + 9
B
0
C
4x2 - 20x + 31
D
4x2 - 20x + 30
উত্তরের বিবরণ
প্রশ্ন: যদি f(x) = 2x - 5 এবং g(x) = x2 + 6 হয় তবে g(f(x)) - 1 এর মান হবে কত?
দেওয়া আছে,
f(x) = 2x - 5
g(x) = x2 + 6
⇒ g(f(x)) = (2x - 5)2 + 6
= 4x2 - 20x + 25 + 6
= 4x2 - 20x + 31
g(f(x)) - 1
= 4x2 - 20x + 31 - 1
= 4x2 - 20x + 30
0
Updated: 1 month ago
একটি সুষম বহুভুজের প্রত্যেকটি বহিঃস্থ কোণের পরিমাণ 30⁰ হলে বহুভুজের বাহুর সংখ্যা কত?
Created: 6 days ago
A
18টি
B
16টি
C
12টি
D
8টি
0
Updated: 6 days ago
২৮ ডিগ্রি কোণের সম্পূরক কোণের পরিমাণ কত?
Created: 4 days ago
A
৬২ ডিগ্রি
B
১১৮ ডিগ্রি
C
৩৩২ ডিগ্রি
D
১৫২ ডিগ্রি
কোনো কোণ এবং তার সম্পূরক কোণ সম্পর্কে মূল ধারণা হলো, দুটি কোণের যোগফল সবসময় ১৮০° হয়। অর্থাৎ, যদি কোনো কোণ জানা থাকে, তাহলে তার সম্পূরক কোণ বের করতে আমরা ১৮০° থেকে সেই কোণটি বিয়োগ করি। এই সূত্রটি খুবই সরল ও প্রাথমিক জ্যামিতির নিয়মের অন্তর্ভুক্ত।
দেওয়া উদাহরণে, মূল কোণ হলো ২৮°। সম্পূরক কোণ বের করার জন্য আমরা ১৮০° থেকে ২৮° বিয়োগ করব:
১৮০° − ২৮° = ১৫২°
এখানেই আমরা পাই উত্তর ১৫২°, যা প্রদত্ত বিকল্পগুলোর মধ্যে ঘ)। এটি দেখায় যে, ২৮° কোণের সঙ্গে যে কোণটি মিলে একসাথে ১৮০° হয়, সেটি সম্পূর্ণরূপে ১৫২°।
এখন কিছু গুরুত্বপূর্ণ বিষয়, যা বোঝা জরুরি:
-
সম্পূরক কোণ বলতে দুটি কোণকে বোঝায় যেগুলোর যোগফল ১৮০°। এটি সাধারণত সোজা কোণ সম্পর্কিত গণনায় ব্যবহার হয়।
-
যেকোনো কোণ X° হলে, তার সম্পূরক কোণ হবে (১৮০° − X°)।
-
উদাহরণ হিসেবে, যদি কোনো কোণ ৯০° হয়, তার সম্পূরক কোণও ৯০° হবে, কারণ ৯০° + ৯০° = ১৮০°।
-
সম্পূরক কোণ শুধুমাত্র প্রথম কোণের সাথে মিলে ১৮০° তৈরি করার জন্য প্রয়োজন, এটি সাধারণত ত্রিভুজ বা বিভিন্ন জ্যামিতিক সমস্যা সমাধানে কাজে আসে।
-
এই নিয়মটি কোণ সংক্রান্ত বিভিন্ন জ্যামিতিক হিসাব যেমন ত্রিভুজের অভ্যন্তরীণ কোণ, বাহ্যিক কোণ বা সমকোণীয় চিত্র বিশ্লেষণে সাহায্য করে।
সুতরাং, ২৮° কোণের সম্পূরক কোণ গণনা করা খুব সরল প্রক্রিয়া: মূল কোণটিকে ১৮০° থেকে বিয়োগ করলে তা পাওয়া যায়। এভাবে আমরা নিশ্চিত করতে পারি যে দুটি কোণের যোগফল সঠিকভাবে ১৮০° হয়েছে।
এটি মূলত শুধু একটি সরল সূত্রের প্রয়োগ, যা সমস্ত প্রাথমিক জ্যামিতি সমস্যায় ব্যবহারযোগ্য। তাই, ২৮° কোণের সম্পূরক কোণ সবসময় ১৫২°, এবং প্রদত্ত বিকল্পের মধ্যে ঘ) সঠিক উত্তর।
এই ধরনের হিসাব শিক্ষার্থীদের কোণ সংক্রান্ত ধারণা শক্তিশালী করতে সাহায্য করে এবং বিভিন্ন জ্যামিতিক সমস্যা সমাধানে সহজীকরণ নিয়ে আসে।
0
Updated: 4 days ago
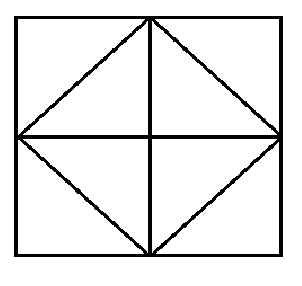
নিম্নোক্ত চিত্রে মোট কয়টি ত্রিভুজ আছে?
Created: 1 month ago
A
৮ টি
B
১০ টি
C
১২ টি
D
১৪ টি
প্রশ্ন: নিম্নোক্ত চিত্রে মোট কয়টি ত্রিভুজ আছে?
সমাধান:
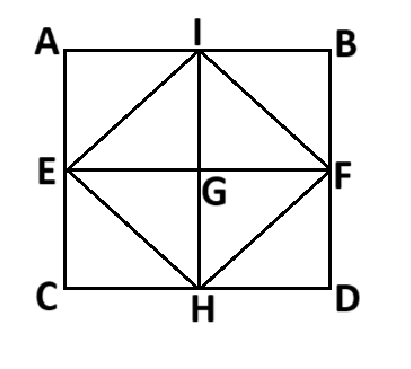
চিত্রটিতে একক ত্রিভুজ অর্থাৎ ত্রিভুজের ভিতরে কোনো বাহু ছেদ করেনি এরূপ ত্রিভুজ- AIE, IEG, ECH, EHG, IBF, IGF, FGH, DFH অর্থাৎ ৮ টি।
আবার,
ত্রিভুজের ভিতর দিয়ে একটি বাহু ছেদ করেছে এরূপ ত্রিভুজ- EIF, EHF, EIH, IFH অর্থাৎ ৪ টি ।
∴ মোট ত্রিভুজ সংখ্যা = (৮ + ৪) টি = ১২ টি
0
Updated: 1 month ago