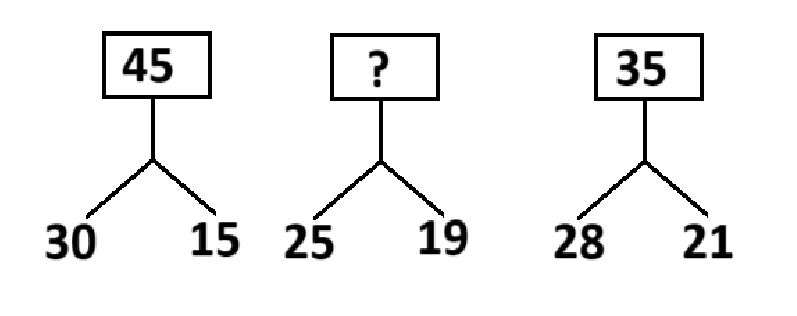
প্রশ্নবোধক স্থানে কোন সংখ্যাটি বসবে?

A
31
B
36
C
38
D
40
উত্তরের বিবরণ
প্রশ্ন: প্রশ্নবোধক স্থানে কোন সংখ্যাটি বসবে?

সমাধান:
নির্ণেয় সংখ্যা = 31
প্রথম চিত্রে,
(30 - 15) + 30
= 15 + 30
= 45
দ্বিতীয় চিত্রে,
(25 - 19) + 25
= 6 + 25
= 31
তৃতীয় চিত্রে,
(28 - 21) + 28
= 7 + 28
= 35
প্রতিটি চিত্রের নিচের সংখ্যাদ্বয়ের বিয়োগফলের সাথে নিচের প্রথম সংখ্যাটি যোগ করলে উপরের চতুর্ভুজের সংখ্যাটি পাওয়া যায়।
0
Updated: 1 month ago
বৃত্তের ব্যাস তিনগুণ করলে ক্ষেত্রফল কতগুণ হবে?
Created: 2 months ago
A
4 গুণ
B
8 গুণ
C
9 গুণ
D
27 গুণ
প্রশ্ন: বৃত্তের ব্যাস তিনগুণ করলে ক্ষেত্রফল কতগুণ হবে?
সমাধান:
ধরি,
বৃত্তের ব্যাস = 2r
∴ বৃত্তের ব্যাসার্ধ = r
∴ বৃত্তের ক্ষেত্রফল = πr2
বৃত্তের ব্যাস তিনগুণ করলে নতুন ব্যাস = (3 × 2r) = 6r
∴ নতুন ব্যাসার্ধ = 6r/2 = 3r
∴ নতুন ব্যাসার্ধ বিশিষ্ট বৃত্তের ক্ষেত্রফল = π(3r)2 = 9 × πr2 = 9 × পূর্বের ব্যাস বিশিষ্ট বৃত্তের ক্ষেত্রফল
অর্থাৎ বৃত্তের ব্যাস তিনগুণ করলে ক্ষেত্রফল 9 গুণ হবে।
0
Updated: 2 months ago
একটি বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য ৮ ফুট হলে, বর্গক্ষেত্রটির ক্ষেত্রফল কত?
Created: 2 months ago
A
১৬ বর্গ ফুট
B
২৪ বর্গ ফুট
C
৩২ বর্গ ফুট
D
৬৪ বর্গ ফুট
সমাধান:
ধরি,
বর্গক্ষেত্রের বাহু = ক ফুট
∴ বর্গক্ষেত্রের কর্ণ = ক√২ ফুট
প্রশ্নমতে,
ক√২ = ৮
⇒ ক = ৮/√২
∴ বর্গক্ষেত্রের ক্ষেত্রফল = (ক)২
= (৮/√২)২
= ৬৪/২
= ৩২ বর্গ ফুট
0
Updated: 2 months ago
১৩ সে.মি ব্যাসার্ধের কেন্দ্র হতে ৫ সে.মি দূরত্বে অবস্থিত জ্যা- এর দৈর্ঘ্য কত?
Created: 1 month ago
A
১২ সে.মি
B
১৬ সে.মি
C
১৮ সে.মি
D
২৪ সে.মি
প্রশ্ন: ১৩ সে.মি ব্যাসার্ধের কেন্দ্র হতে ৫ সে.মি দূরত্বে অবস্থিত জ্যা- এর দৈর্ঘ্য কত?
সমাধান:
আমরা জানি,
সমকোণী ত্রিভুজের বাহুগুলোর অনুপাত হচ্ছে ৫, ১২ ও ১৩
যেখানে,
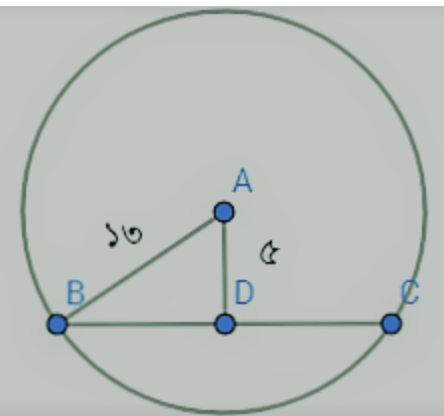
∴ ব্যাসার্ধ = অতিভুজ = ১৩ সে.মি
অর্ধ-জ্যা = ভূমিবাহু = ১২ সে.মি
কেন্দ্র থেকে দূরত্ব = লম্ববাহু = ৫ সে.মি
∴ জ্যা এর দৈর্ঘ্য = ২ × অর্ধ জ্যা
= ২ × ১২ সে.মি
= ২৪ সে.মি।
0
Updated: 1 month ago