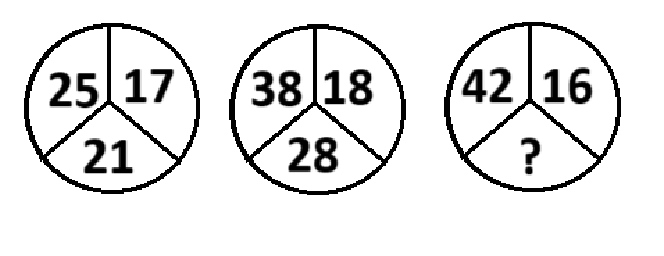
প্রশ্নবোধক স্থানে কোন সংখ্যাটি বসবে?

A
17
B
23
C
29
D
31
উত্তরের বিবরণ
প্রশ্ন: প্রশ্নবোধক স্থানে কোন সংখ্যাটি বসবে?

সমাধান:
নির্ণেয় সংখ্যা = 29
প্রথম চিত্রে,
(25 + 17)/2 = 42/2 = 21
দ্বিতীয় চিত্রে,
(38 + 18)/2 = 56/2 = 28
তৃতীয় চিত্রে,
(42 + 16)/2 = 58/2 = 29
0
Updated: 1 month ago
একটি বর্গক্ষেত্রের ক্ষেত্রফল ৩২৪ বর্গমিটার হলে বর্গক্ষেত্রের পরিসীমা কত?
Created: 2 months ago
A
৪৮ মিটার
B
৬৪ মিটার
C
৭২ মিটার
D
৮৪ মিটার
প্রশ্ন: একটি বর্গক্ষেত্রের ক্ষেত্রফল ৩২৪ বর্গমিটার হলে বর্গক্ষেত্রের পরিসীমা কত?
সমাধান:
দেওয়া আছে,
বর্গক্ষেত্রের ক্ষেত্রফল = ৩২৪ বর্গমিটার
∴ বর্গক্ষেত্রের এক বাহুর দৈর্ঘ্য = √৩২৪ = ১৮ মিটার
আমরা জানি,
বর্গক্ষেত্রের পরিসীমা = ৪ × এক বাহুর দৈর্ঘ্য
= (১৮ × ৪) মিটার
= ৭২ মিটার
0
Updated: 2 months ago
একটি বিন্দু দিয়ে অসংখ্য বৃত্ত আঁকা গেলে দুটি বিন্দু দিয়ে কয়টি বৃত্ত আঁকা যাবে?
Created: 1 week ago
A
অসংখ্য
B
৩টি
C
২টি
D
১টি
প্রশ্নঃ একটি বিন্দু দিয়ে অসংখ্য বৃত্ত আঁকা গেলে দুটি বিন্দু দিয়ে কয়টি বৃত্ত আঁকা যাবে?
সমাধানঃ
ধরা যাক দুটি নির্দিষ্ট বিন্দু A ও B দেওয়া আছে।
একটি বৃত্ত আঁকার জন্য কেন্দ্র ও ব্যাসার্ধ নির্ধারণ করতে হয়।
যে কোনো দুটি বিন্দুর মধ্য দিয়ে এমন অসংখ্য বৃত্ত আঁকা যায়, যেগুলোর ব্যাসার্ধ ভিন্ন হবে কিন্তু উভয় বিন্দু দিয়ে অতিক্রম করবে।
কারণ বৃত্তের কেন্দ্র দুটি বিন্দুর মধ্যবিন্দুর উপর লম্ব অক্ষ রেখার উপর যেকোনো স্থানে হতে পারে।
সুতরাং, দুটি বিন্দু দিয়ে অসংখ্য বৃত্ত আঁকা যায়।
উত্তরঃ ক) অসংখ্য
0
Updated: 1 week ago
একটি সমবাহু ত্রিভুজের বাহুর প্রত্যেকটির দৈর্ঘ্য 2 মিটার বাড়ালে এর ক্ষেত্রফল 3√3 বর্গমিটার বেড়ে যায়। সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য কত?
Created: 2 months ago
A
1 মিটার
B
2 মিটার
C
3 মিটার
D
4 মিটার
প্রশ্ন: একটি সমবাহু ত্রিভুজের বাহুর প্রত্যেকটির দৈর্ঘ্য 2 মিটার বাড়ালে এর ক্ষেত্রফল 3√3 বর্গমিটার বেড়ে যায়। সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য কত?
সমাধান:
মনেকরি,
সমবাহু ত্রিভুজের প্রত্যেক বাহুর দৈর্ঘ্য a মিটার
ত্রিভুজটির ক্ষেত্রফল = √3a2/4
ত্রিভুজের প্রত্যেক বাহুর দৈর্ঘ্য 2 মিটার বাড়ালে ক্ষেত্রফল= √3(a + 2)2/4
প্রশ্নমতে,
{√3(a + 2)2/4} - (√3a2/4) = 3√3
বা, (√3/4){(a + 2)2 - a2} = 3√3
বা, a2 + 4a + 4 - a2 = 12
বা, 4a + 4 = 12
বা, 4a = 8
a = 2
0
Updated: 2 months ago