দোকানের একটি ডিসপ্লে শেলফে থাকা একমাত্র কলমের বাক্সটির অবস্থান বাম দিক থেকে ২৩তম এবং ডান দিক থেকে ১২তম। শেলফটিতে মোট কতটি বাক্স আছে?
A
৩২
B
২৭
C
৩৪
D
৩৮
উত্তরের বিবরণ
প্রশ্ন: দোকানের একটি ডিসপ্লে শেলফে থাকা একমাত্র কলমের বাক্সটির অবস্থান বাম দিক থেকে ২৩তম এবং ডান দিক থেকে ১২তম। শেলফটিতে মোট কতটি বাক্স আছে?
সমাধান:
কলমের বক্সের অবস্থান বাম থেকে ২৩-তম হলে বামদিকে আরও ২২ টি বক্স আছে ।
আবার,
কলমের বক্সের অবস্থান ডান দিক থেকে ১২-তম হলে ডান দিকে আর ১১ টি বক্স রয়েছে।
∴ ঐ শেলফে মোট বক্স আছে = (২২ + ১১ + ১) টি = ৩৪ টি
0
Updated: 1 month ago
একটি অর্ধ-বৃত্ত আকারের জানালার ব্যাস 56 সে.মি. হলে তার পরিসীমা কত?
Created: 1 month ago
A
144 সে.মি. (প্রায়)
B
179 সে.মি. (প্রায়)
C
272 সে.মি. (প্রায়)
D
কোনোটিই নয়
প্রশ্ন: একটি অর্ধ-বৃত্ত আকারের জানালার ব্যাস 56 সে.মি. হলে তার পরিসীমা কত?
সমাধান:
আমরা জানি,
অর্ধবৃত্তের পরিসীমা = বৃত্তের অর্ধ পরিধি + ব্যাস
= πr + 2r
= (22/7) × (56/2) + 56
= (88 + 56)
= 144 সে.মি. (প্রায়)
0
Updated: 1 month ago
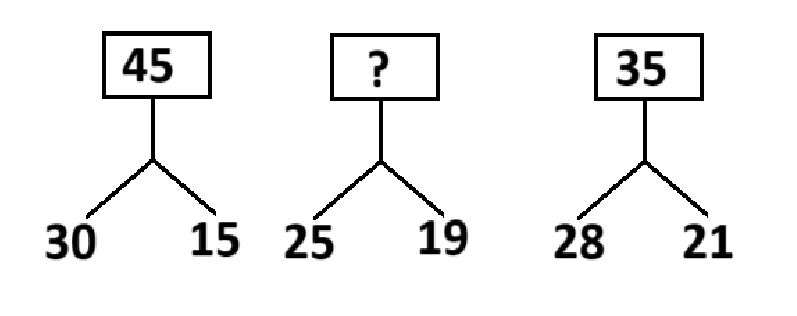
প্রশ্নবোধক স্থানে কোন সংখ্যাটি বসবে?

Created: 1 month ago
A
31
B
36
C
38
D
40
প্রশ্ন: প্রশ্নবোধক স্থানে কোন সংখ্যাটি বসবে?

সমাধান:
নির্ণেয় সংখ্যা = 31
প্রথম চিত্রে,
(30 - 15) + 30
= 15 + 30
= 45
দ্বিতীয় চিত্রে,
(25 - 19) + 25
= 6 + 25
= 31
তৃতীয় চিত্রে,
(28 - 21) + 28
= 7 + 28
= 35
প্রতিটি চিত্রের নিচের সংখ্যাদ্বয়ের বিয়োগফলের সাথে নিচের প্রথম সংখ্যাটি যোগ করলে উপরের চতুর্ভুজের সংখ্যাটি পাওয়া যায়।
0
Updated: 1 month ago
একটি বর্গক্ষেত্রের ক্ষেত্রফল ৮ বর্গমিটার হলে এর কর্ণের দৈর্ঘ্য কত মিটার?
Created: 2 months ago
A
৪ মিটার
B
৬√২ মিটার
C
৮ মিটার
D
৪√২ মিটার
প্রশ্ন: একটি বর্গক্ষেত্রের ক্ষেত্রফল ৮ বর্গমিটার হলে এর কর্ণের দৈর্ঘ্য কত মিটার?
সমাধান:
দেওয়া আছে,
বর্গক্ষেত্রের ক্ষেত্রফল = 8 বর্গমিটার
প্রশ্নমতে,
(বাহু)২ = ৮
⇒ বাহু = √৮
∴ বাহু = ২√২
আমরা জানি,
বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য = √২ × বাহু
= √২ × ২√২
= ৪ মিটার
0
Updated: 2 months ago