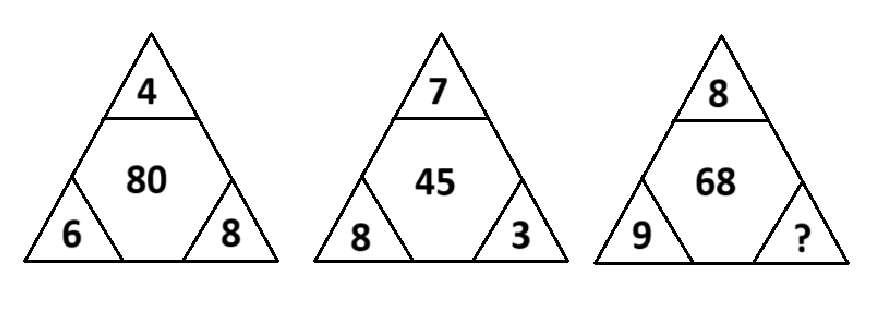
প্রশ্নবোধক চিহ্নিত স্থানে কোন সংখ্যাটি বসবে?

A
3
B
4
C
6
D
9
উত্তরের বিবরণ
প্রশ্ন: প্রশ্নবোধক চিহ্নিত স্থানে কোন সংখ্যাটি বসবে?

সমাধান:
১ম ত্রিভুজে,
(6 + 4) × 8 = 10 × 8 = 80
২য় ত্রিভুজে,
(8 + 7) × 3 = 15 × 3 = 45
এবং ৩য় ত্রিভুজে,
ধরি, সংখ্যাটি = m
∴ (9 + 8) × m = 68
⇒ 17m = 68
⇒ m = 68/17 = 4
0
Updated: 1 month ago
সুষম বহুভুজের বাহুর সংখ্যা n হলে কোণগুলোর সমষ্টি কত?
Created: 1 month ago
A
n সমকোণ
B
(2n + 1) সমকোণ
C
(2n - 1) সমকোণ
D
(2n - 4) সমকোণ
প্রশ্ন: সুষম বহুভুজের বাহুর সংখ্যা n হলে কোণগুলোর সমষ্টি কত?
আমরা জানি,
সুষম বহুভুজের বাহুর সংখ্যা n হলে,
কোণগুলোর সমষ্টি হবে = (2n - 4) সমকোণ ।
0
Updated: 1 month ago
একটি সরলরেখার সাথে আর একটি রশ্মির প্রান্তবিন্দু মিলিত হয়ে যে দুইটি সন্নিহিত কোণ উৎপন্ন হয় তাদের সমষ্টি কত হবে?
Created: 2 months ago
A
৯০°
B
১২০°
C
১৮০°
D
২৭০°
প্রশ্ন: একটি সরলরেখার সাথে আর একটি রশ্মির প্রান্তবিন্দু মিলিত হয়ে যে দুইটি সন্নিহিত কোণ উৎপন্ন হয় তাদের সমষ্টি কত হবে?
সমাধান:
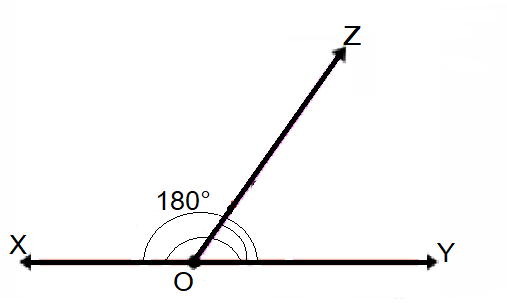
XY সরলরেখার সাথে OZ রশ্মির প্রান্তবিন্দু মিলিত হয়ে ∠XOZ ও ∠YOZ দুটি সন্নিহিত কোণ উৎপন্ন হয় এবং এদের সমষ্টি হবে এক সরলকোণ বা ১৮০ ডিগ্রি।
∴ ∠XOZ + ∠YOZ = ১৮০°
0
Updated: 2 months ago
একই চাপের উপর দণ্ডায়মান কেন্দ্রঃস্থ কোণের পরিমাণ ৯৫° হলে, পরিধিস্থ কোণের পরিমাণ কত হবে?
Created: 4 weeks ago
A
৪২°
B
৪৪.৫°
C
৪৭.৫°
D
১৫০.৫°
সমাধান:
আমরা জানি,
বৃত্তের একই চাপের উপর দণ্ডায়মান পরিধিস্থ কোণ (Inscribed Angle) কেন্দ্রঃস্থ কোণের (Central Angle) অর্ধেক।
দেওয়া আছে,
কেন্দ্রঃস্থ কোণের পরিমাণ = ৯৫°
সুতরাং,
পরিধিস্থ কোণের পরিমাণ = (৯৫° ÷ ২) = ৪৭.৫°
আমরা জানি,
বৃত্তের একই চাপের উপর দণ্ডায়মান পরিধিস্থ কোণ (Inscribed Angle) কেন্দ্রঃস্থ কোণের (Central Angle) অর্ধেক।
দেওয়া আছে,
কেন্দ্রঃস্থ কোণের পরিমাণ = ৯৫°
সুতরাং,
পরিধিস্থ কোণের পরিমাণ = (৯৫° ÷ ২) = ৪৭.৫°
0
Updated: 4 weeks ago