যদি ABC = ZYX হয়, তবে GIVV = ?
A
TERE
B
TEER
C
TREE
D
FREE
উত্তরের বিবরণ
প্রশ্ন: যদি ABC = ZYX হয়, তবে GIVV = ?
সমাধান:

ABC = ZYX
শুরু থেকে ১ম বর্ণ- A শেষ থেকে ১ম বর্ণ- Z
শুরু থেকে ২য় বর্ণ- B শেষ থেকে ২য় বর্ণ- Y
শুরু থেকে ৩য় বর্ণ- C শেষ থেকে ৩য় বর্ণ- X
অনুরুপ প্যাটার্ন মেনেই GIVV = TREE হয়।
0
Updated: 1 month ago
নিচের ক, খ, গ ও ঘ বিকল্প নকশা ৪টির মধ্যে কোনটি প্রশ্নবোধক চিহ্নের স্থানে বসবে?
Created: 1 month ago
A
ক
B
খ
C
গ
D
ঘ
প্রশ্ন: নিচের ক, খ, গ ও ঘ বিকল্প নকশা ৪টির মধ্যে কোনটি প্রশ্নবোধক চিহ্নের স্থানে বসবে?

সমাধান:
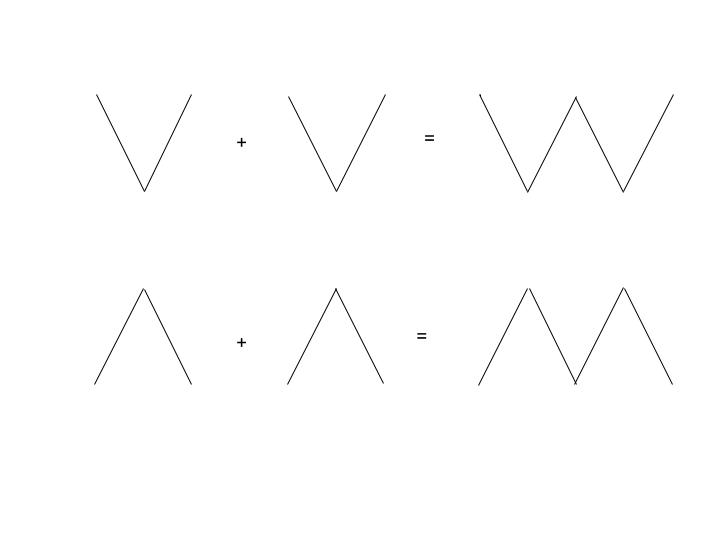
0
Updated: 1 month ago
Telephone : Cable : : Radio:?
Created: 1 month ago
A
Microphone
B
Wireless
C
Electricity
D
Wire
প্রশ্ন: Telephone : Cable : : Radio :?
সমাধান:
Telephone সাধারণত তারযুক্ত (Cable) প্রযুক্তি ছিল।
Radio হলো তারবিহীন (Wireless) প্রযুক্তি।
0
Updated: 1 month ago
১ + ৫ + ৯ + ..............+ ৮১ = ?
Created: 2 months ago
A
৯৬১
B
৮৬১
C
৭৬১
D
৬৬১
প্রশ্ন: ১ + ৫ + ৯ + ..............+ ৮১ = ?
সমাধান:
১ম পদ a = ১,
সাধারণ অন্তর d= ৯ - ৫ = ৪
∴ n-তম পদ = a + (n - 1)d = ৮১
বা, ১ + (n - ১)৪ = ৮১
বা, (n - ১)৪ =.৮০
বা, n - ১ = ২০
∴ n = ২১
∴ সমষ্টি (s) = (n/2){2a + (n - 1)d}
= (২১/২){২ × ১ + (২১ - ১)৪}
= (২১/২)(২ + ৮০)
= (২১/২)× ৮২
= ৮৬১
0
Updated: 2 months ago