একটি
25 মিটার লম্বা মই দেয়ালের সাথে
খাড়া করে রাখা আছে।
মইটির গোড়া দেয়াল থেকে কত দূরে
সরালে এর উপরের অংশ
5 মিটার নিচে নেমে আসবে?
A
13 মিটার
B
10 মিটার
C
18 মিটার
D
15 মিটার
উত্তরের বিবরণ
প্রশ্ন: একটি 25 মিটার লম্বা মই দেয়ালের সাথে খাড়া করে রাখা আছে। মইটির গোড়া দেয়াল থেকে কত দূরে সরালে এর উপরের অংশ 5 মিটার নিচে নেমে আসবে?
সমাধান:
এখানে, AC মইয়ের গোড়া C থেকে D বিন্দুতে সরালে উপরের প্রান্ত A বিন্দু থেকে B বিন্দুতে 5 মিটার নামবে।
মইয়ের দৈর্ঘ্য, AC = BD = 25 মিটার
এবং AB = 5 মিটার
∴ BC = 25 - 5 = 20 মিটার
এখন, পিথাগোরাসের সূত্র অনুযায়ী পাই,
BD2 = BC2 + CD2
⇒ 252 = 202 + CD2
⇒ 625 = 400 + CD2
⇒ CD2 = 625 - 400
⇒ CD2 = 225
⇒ CD = √225
⇒ CD = 15 মিটার
∴ মইটির গোড়া দেয়াল থেকে 15 মিটার দূরে সরালে এর উপরের অংশ 5 মিটার নিচে নেমে আসবে।
0
Updated: 1 month ago
বৃত্তস্থ চতুর্ভুজের একটি কোণ ৯০° হলে উহার বিপরীত কোণের পরিমাণ কত হবে?
Created: 1 month ago
A
৯০°
B
৬০°
C
৩০°
D
১৮০°
প্রশ্ন: বৃত্তস্থ চতুর্ভুজের একটি কোণ ৯০° হলে উহার বিপরীত কোণের পরিমাণ কত হবে?
সমাধান:
আমরা জানি,
বৃত্তস্থ চতুর্ভুজের বিপরীত দুই কোণের সমষ্টি = ১৮০°
একটি কোণ ৯০° হলে,
অপর কোনটি হবে = (১৮০° - ৯০°)
= ৯০°
∴ বিপরীত কোণের পরিমাণ = ৯০°।
0
Updated: 1 month ago
5 সে.মি. ব্যাসার্ধ বিশিষ্ট বৃত্তের কেন্দ্র হতে 4 সে.মি. দূরবর্তী জ্যা এর দৈর্ঘ্য কত?
Created: 2 months ago
A
3 সে.মি.
B
4 সে.মি.
C
5.38 সে.মি.
D
6 সে.মি.
প্রশ্ন: 5 সে.মি. ব্যাসার্ধ বিশিষ্ট বৃত্তের কেন্দ্র হতে 4 সে.মি. দূরবর্তী জ্যা এর দৈর্ঘ্য কত?
সমাধান:
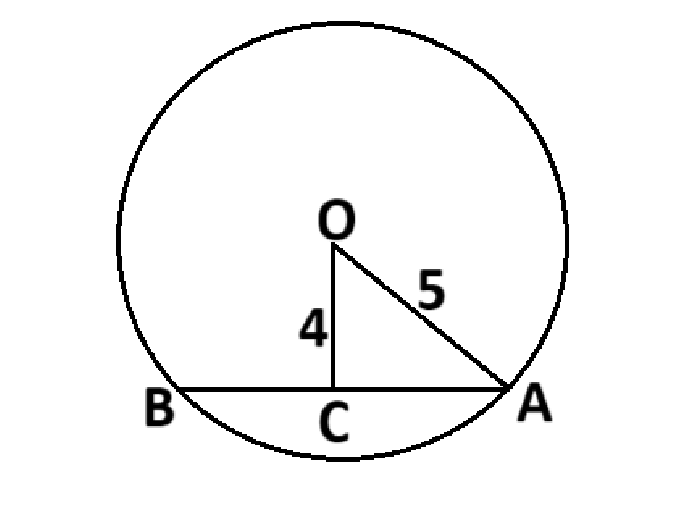
ধরি,
বৃত্তের কেন্দ্র O,
ব্যাসার্ধ = OA = 5 সে.মি.
O বিন্দু হতে AB জ্যা এর দূরত্ব = OC = 4 সে.মি.
OAC সমকোণী ত্রিভুজে,
পিথাগোরাসের উপপাদ্য অনুযায়ী,
OA2 = OC2 + AC2
⇒ AC2 = OA2 - OC2
⇒ AC2 = (5)2 - (4)2
⇒ AC2 = 25 - 16
⇒ AC2 = 9
⇒ AC = 3
C বিন্দু AB জ্যা কে সমদ্বিখণ্ডিত করে।
∴ AC = BC
∴ AB = AC + BC = AC + AC = 2AC
∴ AB = 2AC = (2 × 3) সে.মি. = 6 সে.মি.
0
Updated: 2 months ago
3cm, 4cm এবং 5cm ব্যাসার্ধ বিশিষ্ট তিনটি গোলক গলিয়ে একটি গোলক তৈরি করা হলে গোলকের ব্যাসার্ধ কত?
Created: 1 month ago
A
12 সে.মি.
B
6 সে.মি.
C
4 সে.মি.
D
8 সে.মি.
শ্ন: 3cm, 4cm এবং 5cm ব্যাসার্ধ বিশিষ্ট তিনটি গোলক গলিয়ে একটি গোলক তৈরি করা হলে গোলকের ব্যাসার্ধ কত?
সমাধান:
আমরা জানি,
গোলকের আয়তন = (4/3)πr3
3 সে.মি., 4 সে.মি. ও 5 সে.মি. ব্যাসার্ধ বিশিষ্ট গোলক তিনটির আয়তন যথাক্রমে,
{(4/3)π × 33}, {(4/3)π × 43} {(4/3)π × 53}
সুতরাং নতুন গোলকটির আয়তন ={(4/3)π × 33} + {(4/3)π × 43} + {(4/3)π × 53}
= (4/3)π × (33 + 43 + 53)
= (4/3)π × (27 + 64 + 125)
= (4/3)π × 216
= (4/3)π × 63
∴ নতুন গোলকটির ব্যাসার্ধ = 6 সে.মি.
0
Updated: 1 month ago
