3cm, 4cm এবং 5cm ব্যাসার্ধ বিশিষ্ট তিনটি গোলক গলিয়ে একটি গোলক তৈরি করা হলে গোলকের ব্যাসার্ধ কত?
A
12 সে.মি.
B
6 সে.মি.
C
4 সে.মি.
D
8 সে.মি.
উত্তরের বিবরণ
শ্ন: 3cm, 4cm এবং 5cm ব্যাসার্ধ বিশিষ্ট তিনটি গোলক গলিয়ে একটি গোলক তৈরি করা হলে গোলকের ব্যাসার্ধ কত?
সমাধান:
আমরা জানি,
গোলকের আয়তন = (4/3)πr3
3 সে.মি., 4 সে.মি. ও 5 সে.মি. ব্যাসার্ধ বিশিষ্ট গোলক তিনটির আয়তন যথাক্রমে,
{(4/3)π × 33}, {(4/3)π × 43} {(4/3)π × 53}
সুতরাং নতুন গোলকটির আয়তন ={(4/3)π × 33} + {(4/3)π × 43} + {(4/3)π × 53}
= (4/3)π × (33 + 43 + 53)
= (4/3)π × (27 + 64 + 125)
= (4/3)π × 216
= (4/3)π × 63
∴ নতুন গোলকটির ব্যাসার্ধ = 6 সে.মি.
0
Updated: 1 month ago
একটি সমকোণী ত্রিভুজের সমকোণ ব্যতীত অপর দুইটি কোণের পার্থক্য 20 ডিগ্রি হলে ক্ষুদ্রতম কোণটির মান কত?
Created: 1 month ago
A
30°
B
35°
C
48°
D
39°
প্রশ্ন: একটি সমকোণী ত্রিভুজের সমকোণ ব্যতীত অপর দুইটি কোণের পার্থক্য 20 ডিগ্রি হলে ক্ষুদ্রতম কোণটির মান কত?
সমাধান:
ধরি,
অপর দুইটি কোণের মধ্যে ক্ষুদ্রতম কোণ = x°
তাহলে বৃহত্তম কোণ = (x + 20)°
প্রশ্নমতে,
x° + (x + 20)° + 90° = 180°
⇒ 2x° + 20° + 90° = 180°
⇒ 2x° + 110 = 180°
⇒ 2x° = 70°
⇒ x° = 35°
সুতরাং, ক্ষুদ্রতম কোণ = 35°
0
Updated: 1 month ago
দুটি বর্গের ক্ষেত্রফলের অনুপাত 36 : 81। তাদের পরিসীমার অনুপাত কত?
Created: 2 months ago
A
9 : 8
B
2 : 3
C
3 : 2
D
5 : 7
প্রশ্ন: দুটি বর্গের ক্ষেত্রফলের অনুপাত 36 : 81। তাদের পরিসীমার অনুপাত কত?
সমাধান:
ধরি,
প্রথম বর্গের বাহু = a
এবং দ্বিতীয় বর্গের বাহু = b
প্রশ্নমতে,
a2 : b2 = 36 : 81
⇒ a : b = √36 : √81 [উভয় দিকের বর্গমূল নিলে পাই]
⇒ a : b = 6 : 9
∴ a : b = 2 : 3...........(1)
আমরা জানি,
বর্গক্ষেত্রের পরিসীমা = 4 × বাহু
∴ পরিসীমার অনুপাত = 4a : 4b
= a : b
= 2 : 3 [(1) নং হতে]
অতএব, দুটি বর্গের ক্ষেত্রফলের অনুপাত 36 : 81 হলে, তাদের পরিসীমার অনুপাত = 2 : 3 হবে।
0
Updated: 2 months ago
একটি সমবাহু ত্রিভুজের শীর্ষবিন্দু থেকে ভর কেন্দ্রের দূরত্ব 14 সে.মি. হলে ত্রিভুজটির মধ্যমা কত?
Created: 2 months ago
A
18 সে.মি.
B
20 সে.মি.
C
21 সে.মি.
D
24 সে.মি.
প্রশ্ন: একটি সমবাহু ত্রিভুজের শীর্ষবিন্দু থেকে ভর কেন্দ্রের দূরত্ব 14 সে.মি. হলে ত্রিভুজটির মধ্যমা কত?
সমাধান:
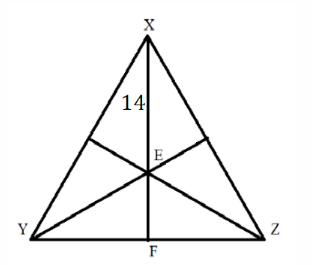
আমরা জানি
ত্রিভুজের মধ্যমাত্রয় যে বিন্দুতে মিলিত হয় সেই বিন্দুকে ঐ ত্রিভুজের ভরকেন্দ্র বলে।
∴ EX : EF = 2 : 1
⇒ 14 : EF = 2 : 1
⇒ 14/EF = 2/1
⇒ 2EF = 14
⇒ EF = 14/2
⇒ EF = 7
∴ ত্রিভুজটির মধ্যমা = FX = EX + EF = 14 + 7 = 21 সে.মি.
0
Updated: 2 months ago