PQR ত্রিভুজের PN একটি মধ্যমা এবং M ভরকেন্দ্র। যদি মধ্যমা PN-এর দৈর্ঘ্য ২১ সেমি হয়, তাহলে PM-এর দৈর্ঘ্য কত?
A
১৪ সেমি
B
২১ সেমি
C
৩৬ সেমি
D
১৮ সেমি
উত্তরের বিবরণ
প্রশ্ন: PQR ত্রিভুজের PN একটি মধ্যমা এবং M ভরকেন্দ্র। যদি মধ্যমা PN-এর দৈর্ঘ্য ২১ সেমি হয়, তাহলে PM-এর দৈর্ঘ্য কত?
সমাধান:
আমরা জানি,
কোনো ত্রিভুজের ভরকেন্দ্র তার মধ্যমাকে ২ : ১ অনুপাতে বিভক্ত করে।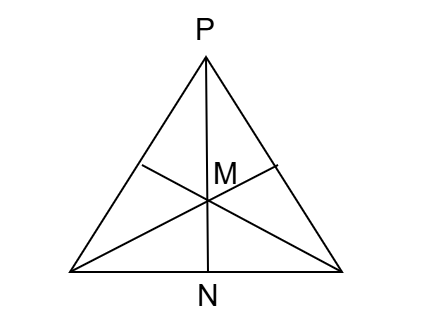
এখানে,
PN মধ্যমা এবং M ভরকেন্দ্র।
∴ PM : MN = ২ : ১
মোট অনুপাত = ২ + ১ = ৩
মধ্যমা PN-এর দৈর্ঘ্য = ২১ সেমি
ভরকেন্দ্র M, মধ্যমা PN-কে দুটি অংশে বিভক্ত করেছে: PM এবং MN।
∴ PM-এর দৈর্ঘ্য = ২১ এর (২/৩) অংশ
= ২১ × (২/৩) সেমি
= ১৪ সেমি
সুতরাং, PM-এর দৈর্ঘ্য ১৪ সেমি।
0
Updated: 1 month ago
৪ টাকায় ১ টি করে কলা ক্রয় করে ৬০ টাকায় কয়টি কলা বিক্রয় করলে ২৫% লাভ হবে?
Created: 1 month ago
A
২০ টি
B
১০ টি
C
১৫ টি
D
১২ টি
প্রশ্ন: ৪ টাকায় ১ টি করে কলা ক্রয় করে ৬০ টাকায় কয়টি কলা বিক্রয় করলে ২৫% লাভ হবে?
সমাধান:
২৫% লাভে, ১ টি কলার বিক্রয়মূল্য = ৪ + ৪ এর ২৫%
= ৪ + ১ টাকা
= ৫ টাকা
অর্থাৎ, ৫ টাকায় বিক্রয় করতে হবে ১ টি
১ টাকায় বিক্রয় করতে হবে ১/৫ টি
∴ ৬০ টাকায় বিক্রয় করতে হবে ৬০/৫ টি
= ১২ টি
0
Updated: 1 month ago
42 ফুট লম্বা একটি খুঁটি এমনভাবে ভেঙ্গে গেলো যে তা সম্পূর্ণভাবে বিচ্ছিন্ন না হয়ে ভূমির সাথে 30° কোণ উৎপন্ন করে। খুঁটিটি কত উঁচুতে ভেঙ্গেছিল?
Created: 1 month ago
A
14
B
15
C
16
D
17
প্রশ্ন: 42 ফুট লম্বা একটি খুঁটি এমনভাবে ভেঙ্গে গেলো যে তা সম্পূর্ণভাবে বিচ্ছিন্ন না হয়ে ভূমির সাথে 30° কোণ উৎপন্ন করে। খুঁটিটি কত উঁচুতে ভেঙ্গেছিল?
সমাধান: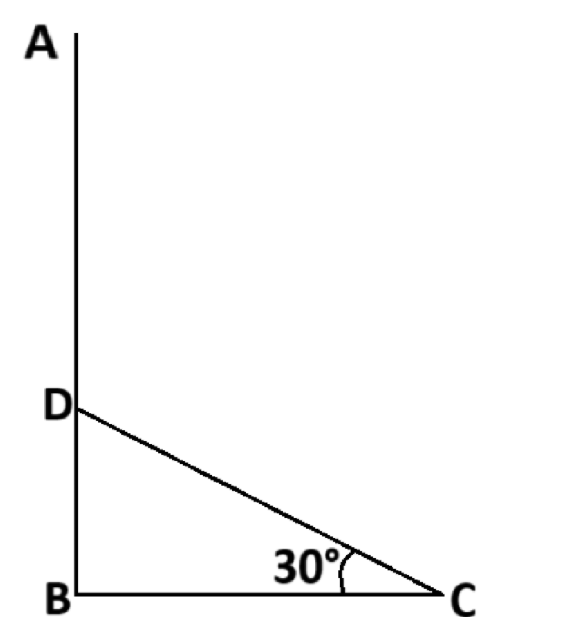
চিত্রে AB = 42 ফুট
এবং AD = DC = 42 - BD
প্রশ্নমতে,
sin 30° = BD/DC
⇒ 1/2 = BD/(42 - BD)
⇒ 2BD = 42 - BD
⇒ 3BD = 42
⇒ BD = 42/3 = 14 ফুট
0
Updated: 1 month ago
একটি ট্রাপিজিয়ামের সমান্তরাল বাহু দুইটি যথাক্রমে 12 সে.মি. ও 9 সে.মি. এবং লম্ব দূরত্ব 4 সে.মি.। ট্রাপিজিয়ামটির ক্ষেত্রফল কত?
Created: 2 months ago
A
7.5 বর্গ সে.মি.
B
21 বর্গ সে.মি.
C
42 বর্গ সে.মি.
D
21√2 বর্গ সে.মি
গণিত
ঘন জ্যামিতি (Solid geometry)
জ্যামিতি (geometry)
জ্যামিতি প্রাথমিক ধারণা (Basic Concept)
ত্রিভুজ (Triangle)
সমাধান:
দেওয়া আছে,
ট্রাপিজিয়ামের সমান্তরাল দুই বাহু 12 সে.মি. ও 9 সে.মি.
লম্ব দূরত্ব = 4 সে.মি.
আমরা জানি,
ট্রাপিজিয়ামের ক্ষেত্রফল = (1/2) × সমান্তরাল বাহু দুইটির সমষ্টি × উচ্চতা
= (1/2) × (12 + 9) × 4 বর্গ সে.মি.
= (1/2) × 21 × 4 বর্গ সে.মি.
= 42 বর্গ সে.মি.
0
Updated: 2 months ago