সমাধান:

জ্যামিতির সূত্র অনুযায়ী, একই চাপের উপর দাঁড়ানো বৃত্তস্থ কোণ হলো কেন্দ্রস্থ কোণের অর্ধেক।

অতএব,

$$\text{বৃত্তস্থ কোণ} = \tfrac{1}{2} \times 72^\circ = 36^\circ$$

উত্তর: ৩৬° ✅

প্রশ্ন: tanA = 4/3 হলে, sinA= ?

সমাধান: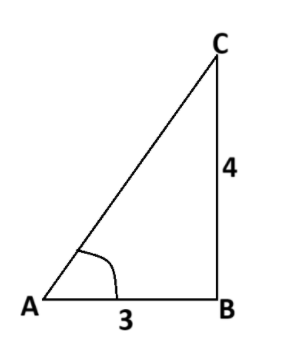

দেওয়া আছে,
tanA = 4/3

A কোণের বিপরীত বাহু = 4,
সন্নিহিত বাহু = 3

এখন,
অতিভুজ2 = 42 + 32 
⇒ অতিভুজ2 = 16 + 9
⇒ অতিভুজ2 =25
⇒ অতিভুজ =√25
⇒ অতিভুজ = 5

সুতরাং, sinA = লম্ব/অতিভুজ = 4/5

প্রশ্ন: একটি গাছের পাদদেশ হতে 26√3 মিটার দূরে একটি স্থানে গাছটির শীর্ষের উন্নতি কোণ 30° হলে, গাছটির উচ্চতা কত মিটার?

সমাধান:

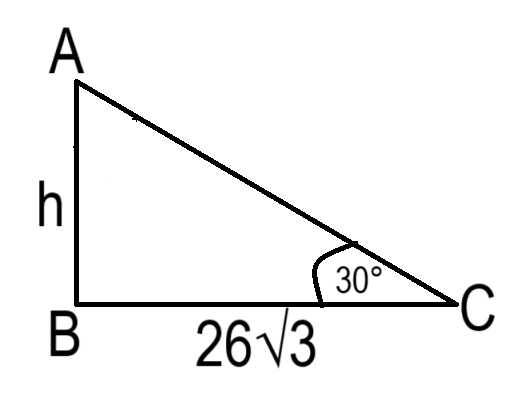
এই সমস্যাটি সমাধান করার জন্য ত্রিকোণমিতির tan অনুপাত ব্যবহার করতে হবে। 
ধরি, 
গাছটির উচ্চতা = h মিটার
গাছের পাদদেশ থেকে দূরবর্তী স্থানের দূরত্ব = 26√3 মিটার
গাছটির শীর্ষের উন্নতি কোণ = 30°. 

আমরা জানি,
tanθ = (লম্ব/ভূমি) 
এখন,
⇒ tan30° = গাছটির উচ্চতা/গাছটির পাদদেশ থেকে দূরবর্তী স্থানের দূরত্ব
⇒ tan(30°) = h/26√3 
⇒ 1/√3 = h/26√3
⇒ h = (1/√3)(26√3)
∴ h = 26 মিটার

∴  গাছটির উচ্চতা = 26 মিটার